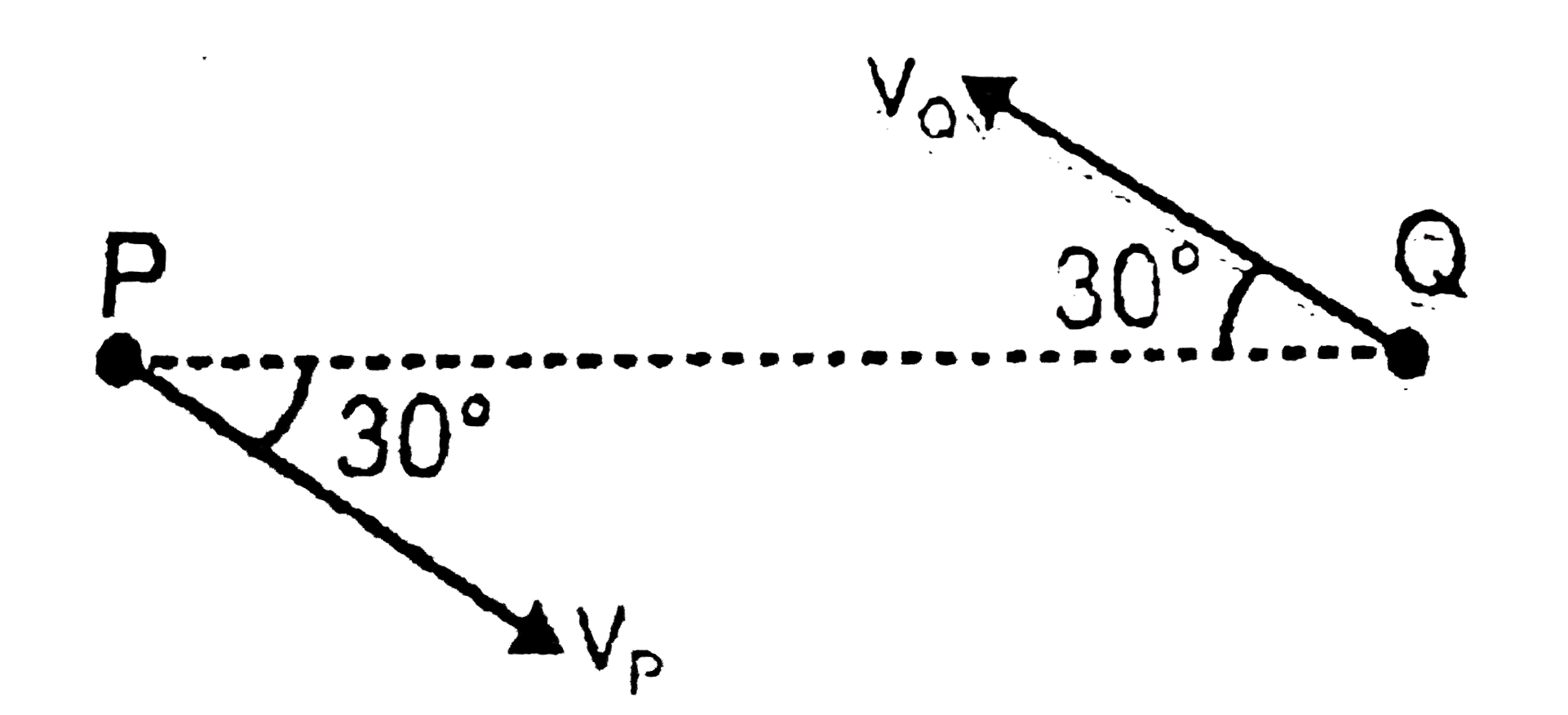Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two moving particles P and Q are 10cm apart at any instant. Velocity ...
Text Solution
|
- Two particles P and Q simultaneously start moving from point A with ve...
Text Solution
|
- Two moving particles P and Q are 10 m apart at a certain instant. The ...
Text Solution
|
- A particle is moving with uniform acceleration along a straight line. ...
Text Solution
|
- Two particles P and Q are moving as shown in the figure. At this momen...
Text Solution
|
- Two moving particles P and Q are apart at any instant. Velocity of P i...
Text Solution
|
- A particle P is moving along a straight line with a velocity of 3ms^(-...
Text Solution
|
- Two moving particles P and Q are 10 m apart at a certain instatn. The ...
Text Solution
|
- To particles P and Q are initially 40 m apart P behind Q. Particle P s...
Text Solution
|