Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
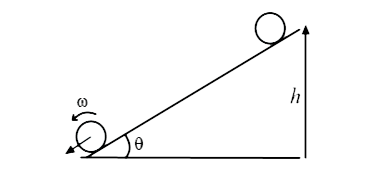
- A solid cylinder rolls down an inclined plane of height h and inclinat...
Text Solution
|
- A solid cylinder rolls down an inclined plane of height h and inclinat...
Text Solution
|
- A solid cylinder of mass M and radius R rolls down an inclined plane o...
Text Solution
|
- A solid cylinder of mass M and radius R rolls down an inclined plane o...
Text Solution
|
- If a hollow cylinder and a solid cylinder are allowed to roll down an ...
Text Solution
|
- A sphere rolls down an inclined plane of inclination theta . What is t...
Text Solution
|
- For a hollow cylinder and a solid cylinder rolling without slipping on...
Text Solution
|
- For a hollow cylinder and a solid cylinder rolling without slipping on...
Text Solution
|
- A solid cylinder rolls down from an inclined plane of height h. What i...
Text Solution
|