Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
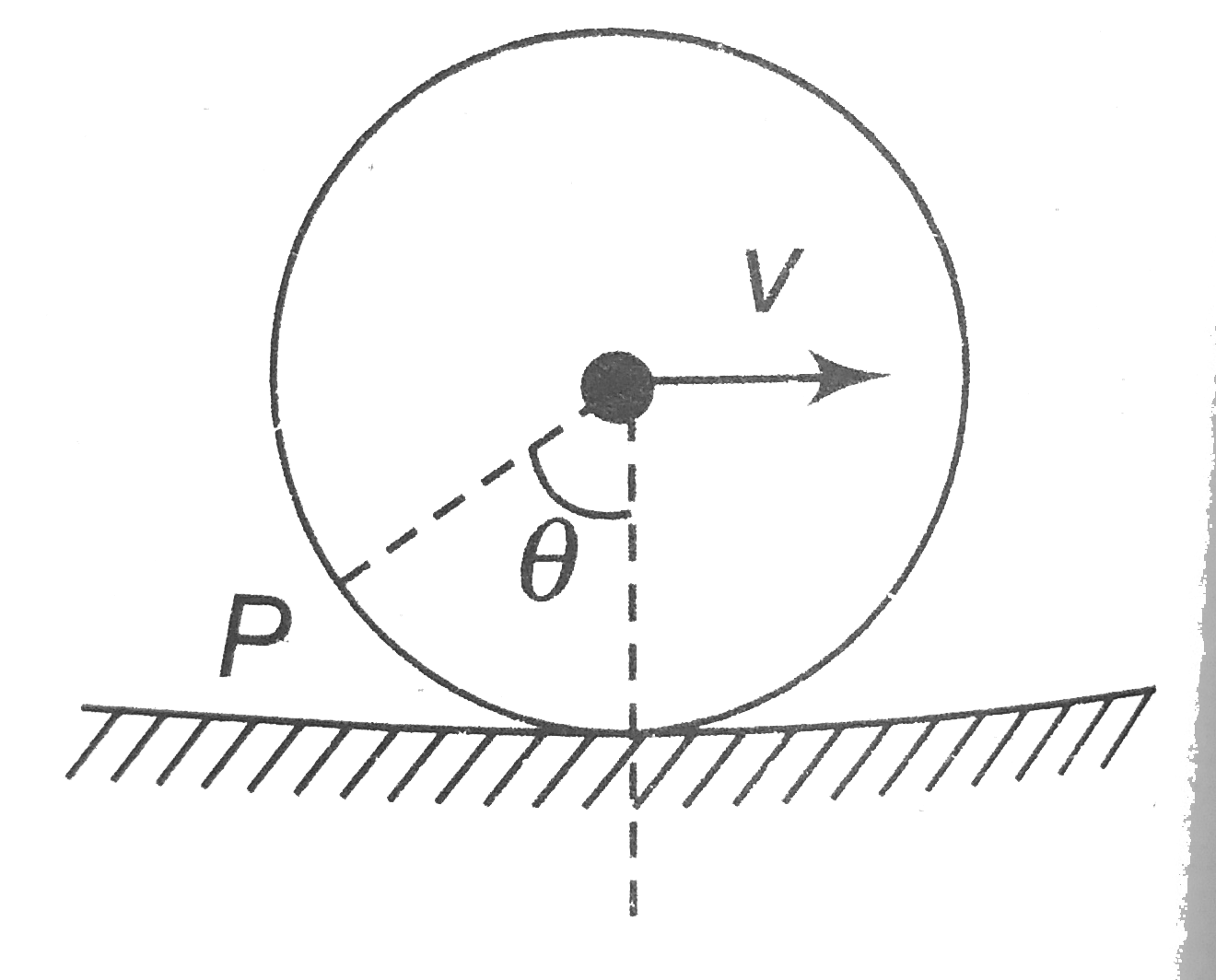
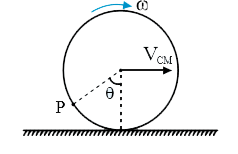
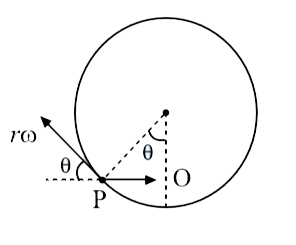
- A hoop rolls on a horizontal ground without slipping with linear speed...
Text Solution
|
- A small body A is fixed to the inside of a thin rigid hoop of radius R...
Text Solution
|
- A hoop rolls on a horizontal ground without slipping with linear speed...
Text Solution
|
- A hoop and a solid cylinder have the same mass and radius. They both r...
Text Solution
|
- A ring rolls without slipping on the ground. Its centre C moves with a...
Text Solution
|
- A small body A is fixed to the inside of a thin rigid hoop of radius R...
Text Solution
|
- A wheel is rolling straight on ground without slipping. If the axis of...
Text Solution
|
- A disc rolls on ground without slipping . Velocity of centre of mass i...
Text Solution
|
- If a loop of chain is spunat high speed, it will roll like a hoop with...
Text Solution
|