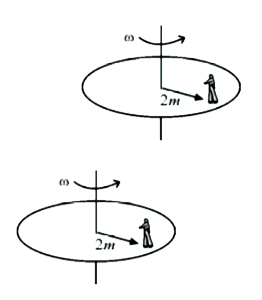
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A turntable turns about a fixed vertical axis, making one revolution i...
Text Solution
|
- A turntable turns about a fixed vertical axis, making one revolution i...
Text Solution
|
- A man of mass 100 kg stands at the rim of a turtable of radius 2 m and...
Text Solution
|
- A 60.0-kg woman stands at the western rim of a horizontal turntable ha...
Text Solution
|
- If a constant torque of 500 N-m turns a wheel of moment of inertia 100...
Text Solution
|
- A uniform rod is fixed to a rotating turntable so that its lower end i...
Text Solution
|
- A constant torque of 400Nm turns a wheel of moment of inertia 100kg m^...
Text Solution
|
- Calculate the moment of inertia of a solid sphere of mass 10 kg and ra...
Text Solution
|
- A disc of radius 10 cm can rotate about an axis passing through its ce...
Text Solution
|