Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
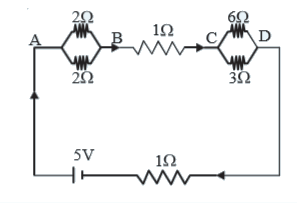
- A network of resistors is connected to a 5 V battery with internal res...
Text Solution
|
- A network of resistances is connected to a 16 V battery with internal ...
Text Solution
|
- A network of resistances is connected to a 16 V battery with internal ...
Text Solution
|
- चित्र 3 .17 में दिखाए गए अनुसार 1 Omega आंतरिक प्रतिरोध के 16V ...
Text Solution
|
- A network of resistor is connected to a 16 V battery with internal res...
Text Solution
|
- A network of resistor is connected to a 16 V battery with internal res...
Text Solution
|
- A network of resistor is connected to a 16 V battery with internal res...
Text Solution
|
- चित्र में दर्शाए अनुसार 1Omega आन्तरिक प्रतिरोध की 16V की एक बैटरी से ...
Text Solution
|
- A network of resistors is connected to a 5 V battery with internal res...
Text Solution
|