A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
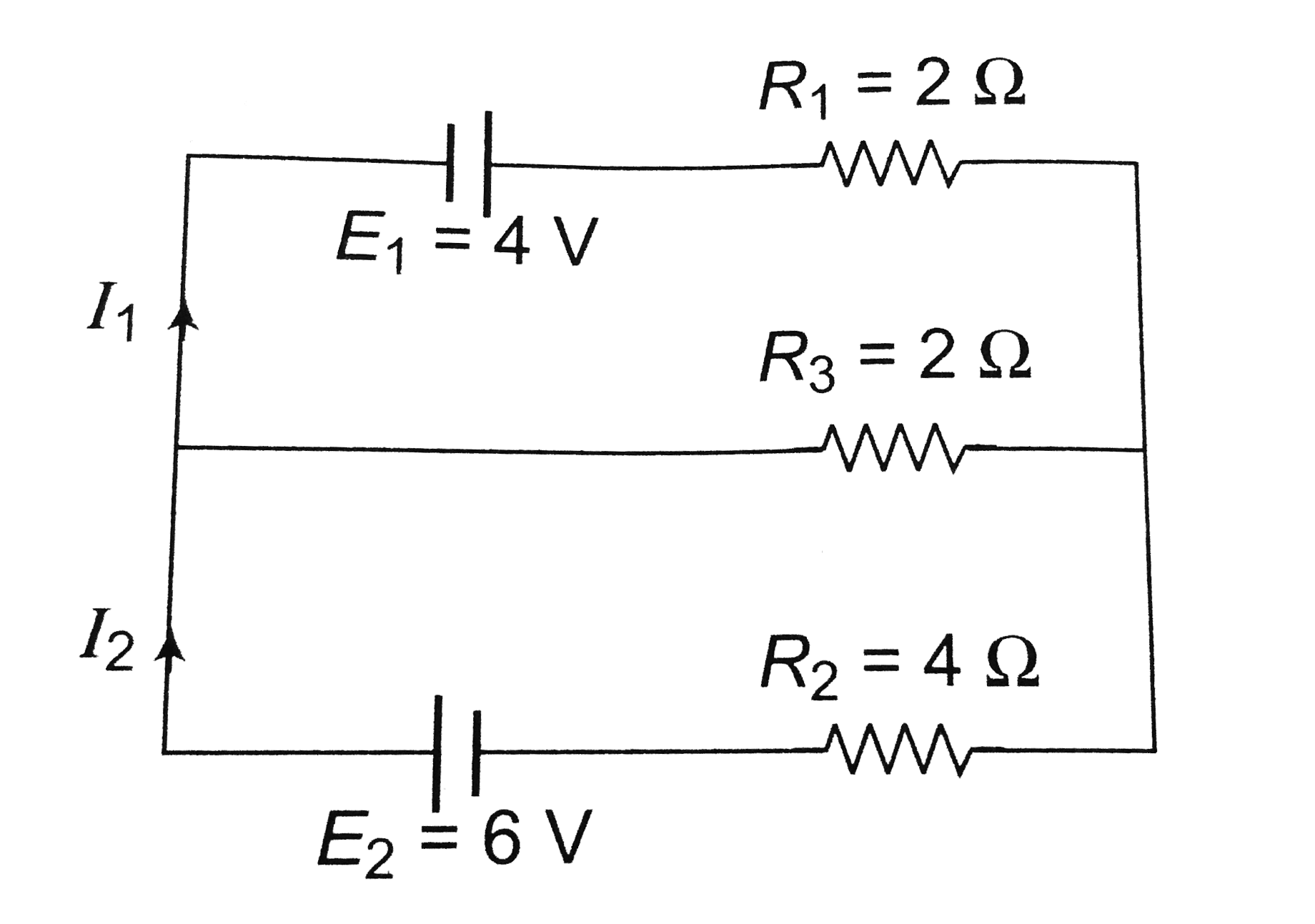
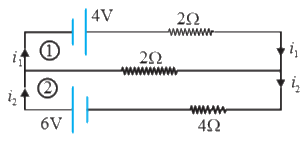
- In the circuit shown below E(1) = 4.0 V, R(1) = 2 Omega, E(2) = 6.0 V,...
Text Solution
|
- In the circuit shows in Fig E = 15 V, R(1) = 1Omega, R(2) = 1 Omega, R...
Text Solution
|
- In the circuit shows in Fig E = 15 V, R(1) = 1Omega, R(2) = 1 Omega, R...
Text Solution
|
- In the network shown the potential difference between A and B is (R = ...
Text Solution
|
- In the circuit shown below E(1) = 4.0 V, R(1) = 2 Omega, E(2) = 6.0 V,...
Text Solution
|
- In the circuit R(1) = 4 Omega , R(2) = R(3) = 15 Omega R(4) = 30 Omega...
Text Solution
|
- Find a potentail difference varphi(1) - varphi(2) between points 1 and...
Text Solution
|
- In the circuit shown in Fig. the emf of the sources is equal to xi = ...
Text Solution
|
- Find the magnitude and direction of the current flowing through the ...
Text Solution
|