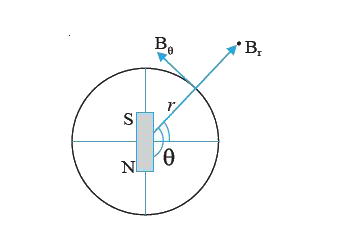
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Considering the earth as a short magnet with its centre coinciding wit...
Text Solution
|
- Let the magnetic field on earth be modelled by that of a point magneti...
Text Solution
|
- Considering the earth as a short magnet with its centre coinciding wit...
Text Solution
|
- Considering the earth's magnetism to be due to a very powerful short m...
Text Solution
|
- Let the magnetic field on earth be modeled by that of a point magneti...
Text Solution
|
- 43.nIf at any place,the angle of dip is theta and magnetic latitude is...
Text Solution
|
- At a place the true value of angle of dip is 60^(@). If dip circle is ...
Text Solution
|
- Let the magnetic field on earth be modelled by that of a point magneti...
Text Solution
|
- Angle of dip delta and latitude lambda on earth's surface are related ...
Text Solution
|