Home
Class 10
MATHS
Prove that " the ratio of areas of two s...

Prove that " the ratio of areas of two similar triangles is equal to the square of the ratio of their altitudes.

Promotional Banner

Topper's Solved these Questions

  • MOST LIKELY QUESTION PAPER 9

    CPC CAMBRIDGE PUBLICATION|Exercise VI. Answer the following Questions :|1 Videos

  • MOST LIKELY QUESTION PAPER 9

    CPC CAMBRIDGE PUBLICATION|Exercise IV. Answer the following Questions :|6 Videos

  • MODEL QUESTION PAPER 7

    CPC CAMBRIDGE PUBLICATION|Exercise QUESTIONS|37 Videos

  • MOST LIKELY QUESTION PAPER 10

    CPC CAMBRIDGE PUBLICATION|Exercise QUESTIONS|36 Videos

Similar Questions

Explore conceptually related problems

Prove that “the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides”.

Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.

Prove that the ratio at the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.

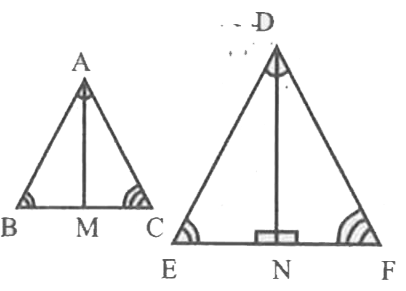
What is the ratio of areas of two similar triangles whose sides are in the ratio 15 : 19 ?

Prove that if the area of similar triangles are equal, they are congruent.

If the areas of two similar triangles are equal , prove that they are congruent.

If the area of the similar triangles are equal, then they are congruent. Prove.

In an equilateral triangle , prove that three times the square pf one side is equal to four times the square of one of its altitudes.

If the areas of two-similar triangles are equal, prove that the they are congruent.

Prove that the ratio of the area of a circle and the equilateral triangle whose side is equal to the diameter of the circle is pi:sqrt3