Properties of scalar product are :
(i) The product quantity `vec(A), vec(B)` is always a sxalar. It is positive if the angle between the vectors is acule (i.e., `theta lt 90^(@)` . It is negative if the angle between them is obtuse (i.e., `90^(@) lt theta lt 180^(@) ` )
(ii) The scalar product obeys commutative law i.e., `vec(A). vec(B) = vec(B). vec(A)`
(iii) The vectors obeys distributive law i.e., `vec(A) . (vec(B) + vec(C)) = vec(A) . vec(B) + vec(A) . vec(C)`
(iv) The angle between the vectors ,
`theta = cos^(-1)[(vec(A).vec(B))/(AB)]`
(v) The scalar product of two vectors will be maximum when `cos theta = 1, i.e. theta = 0^(@), "so" (vec(A) . vec(B))_("max") = AB`
(vi) The scalar product of two vectors will be minimum, when ` cos theta = - 1, i.e., theta = 180^(@)` . When the vectors are anti-parallel.
`(vec(A). vec(B))_("min") = - AB`
(vii) If two vectors `vec(A) and vec(B)` are perpendicular to each other then their scalar product `vec(A) . vec(B) = 0 ` , because `cos 90^(@) = 0` . Then the vectors `vec(A) and vec(B)` are said to be mutually orthogonal .
(viii) The scalar product of a vector with itself is termed as self-dot product. It is given by `(vec(A))^(2) = vec(A) . vec(A) = A A cos theta = A^(2)` . Here angle `theta = 0^(@)`
The magnitude of the vector is given by `vec(A) is |vec(A)| = A = sqrt(A) . vec(A)`
(ix) In case of a unit vector , `hat (n)`
` hat (n) . hat(n) = 1 xx 1 xx cos 0 = 1 ` . For example, ` hat (i) . hat (i) = hat (j) . hat (j)= hat (k) . hat (k) = `
(x) In the case of orthogonal unit vectors `hat (i) . hat (j) and hta(k)` ,
`hat (i). hat(j) = hat(j) . hat (k) = hat(k) . hat (i) = 1.1 cos 90^(@) = 0 `
(xi) In terms of components the scalar product of ` vec(A) and vec(B)` can be written as
`vec(A) . vec(B) = (A, hat (i) + A hat(j) + A, hat(k)).(B, hat(i) + B, hat(j) + B, hat(k))`
` = A_(x) B_(x) + A_(y) B_(y) + A_(z) B_(z)`, With all other terms zero.
The magnitude of vector `|vec(A)|` is given by
`|vec(A)| = A = sqrt(A_(x)^(z)+A_(y)^(2)+A_(z)^(2))`
Properties of vector (cross) product are :
(i) The vector product of any two vectors is always another vector whose direction is perpendicular to the piane containing these two vectors , i.e., orthogonal to both the vectors `vec(A) and vec(B)` . In this case. the vectors `vec(a) and vec(B)` may or may not be mutually othogonal .
(ii) The vector of two vectors is not commutative, i.e., `vec(A) xx vec(B) ne vec(B) xx vec(A) ` But ., `vec(A) xx vec(B) = - [ vec(B) xx vec(A)]`.
But , `|vec(A) xx vec(B)| = |vec( B) xx vec(A)| = AB sin theta i.e., ` in the case of the product vectors `vec(A) xx vec(B) and vec(B) xx vec(A)` , the magnitudes are equal but directions are opposite to each other .
(iii) The vector product of two vectors will have maximum magnitude when sin `theta = 1, i.e., theta = 90^(@)` i.e., when the vectors `vec(A) and vec(B)` are orthogonal to each other .
`(vec(A) xx vec(B))_("max") = AB hat(n)`
(iv) The vector product of two non-zero vectors will be minimum when `|sin theta| = 0, i.e., theta = 0^(@) or 180^(@)`
`(vec(A) xx vec(B))_("min") = 0 `
If the vectors are either parallel or anti parallel i.e., then the vector product of two non-zero vectors vanishes.
(v) The self - cross product, i.e., product of a vector with itself is the null vector
`vec(A) xx vec(A) = A A sin 0^(@) hat(n) = vec(0)`
The null vector `vec(0)` is simple denoted as zero in physics.
(vi) The self-vector products of unit vectors are thus zero .
`hat(i) xx hat (i) = hat(j) xx hat (j) = hat (k) xx hat (k) = vec(0)`
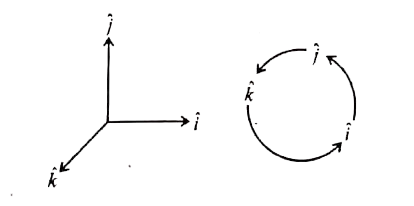
(vii) In the case of orthogonal unit vectors, `hat(i), hat(j), hat(k)` in accordance with the right hand screw rule
`hat (i) xx hat(j) = hat (k), hat(j) xx hat (k) = hat(i) and hat (k) xx hat (i) = hat(j)`
Also, since the cross product is not commutative,
`hat(j) xx hat(i) = - hat(k), hat(k) xx hat(j) = - hat(i) and hat(i) xx hat(k) = - hat(j)`
(viii) In terms of components the vector product of two vectors `vec(A) and vec(B)` is `vec(A) xx vec(B)=|{:(hat(i),hat(j),hat(k)),(A_(x),A_(y),A_(z)),(B_(x),B_(y),B_(z) ):}|`
`{{:(hat(i)(A_(y)B_(z)-A_(z)B_(y))),(+hat(j)(A_(z)B_(x)-A_(x)B_(z))),(+hat(k)(A_(x)B_(y)-A_(y)B_(x))):}`
Note that in the `hat(j)^(th)` component the order of multiplication is different than `hat(i)^(th) and hat(k)^(th)` components .
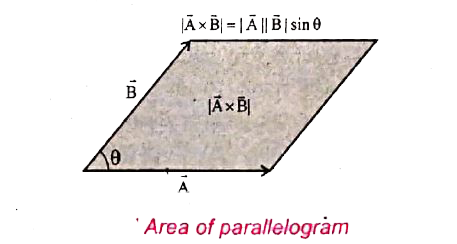
(ix) If two vectors `vec(A) and vec(B)` form adjacent sides in a parallelogram, then the magnitude of `|vec(A) xx vec(B)|` will give the area of the parallelogram as represented graphically in the figure.
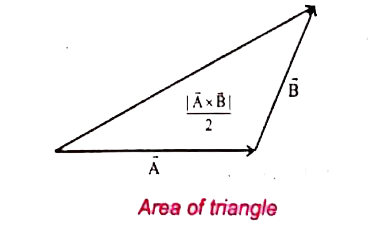
(x) Since a parallelogram is divided into two equal triangles as shown in the figure, the area of a triangle with `vec(A) and vec(B)` as sides is `(1)/(2) |vec(A) xx vec(B)|`.