Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
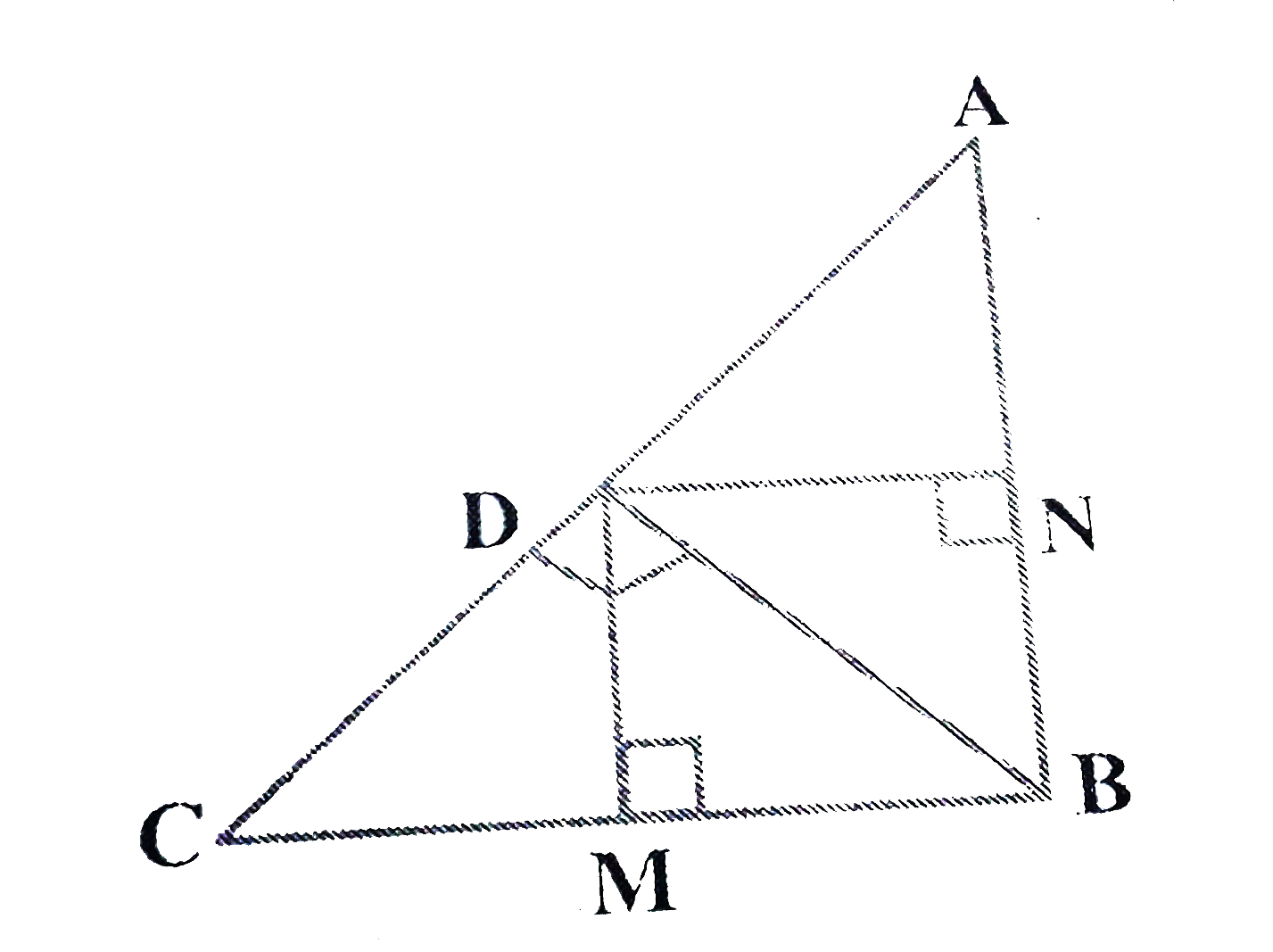
- In fig., D is a point on hypotenuse AC of DeltaA B C ,D M|B Cand D N...
Text Solution
|
- In fig., D is a point on hypotenuse AC of DeltaA B C ,D M|B Cand D N...
Text Solution
|
- A B C D is a parallelogram. L\ a n d\ M are points on A B\ a n d\ D C ...
Text Solution
|
- In Figure, M ,\ N\ a n d\ P are the mid-points of A B ,\ A C\ a n d\ B...
Text Solution
|
- A B C D is a trapezium in which A B|\|D C , M\ a n d\ N are the mid-...
Text Solution
|
- In fig., D is a point on hypotenuse AC of DeltaA B C ,D M|B Cand D N...
Text Solution
|
- In Figure, /B C D=/A D C and /A C B=/B D Adot Prove that A D=B C and /...
Text Solution
|
- In Figure, A B C is a right triangle right angled at B and D is the ...
Text Solution
|
- A B C D is a rectangle. Points M and N are on B D such that A M|B D...
Text Solution
|