Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
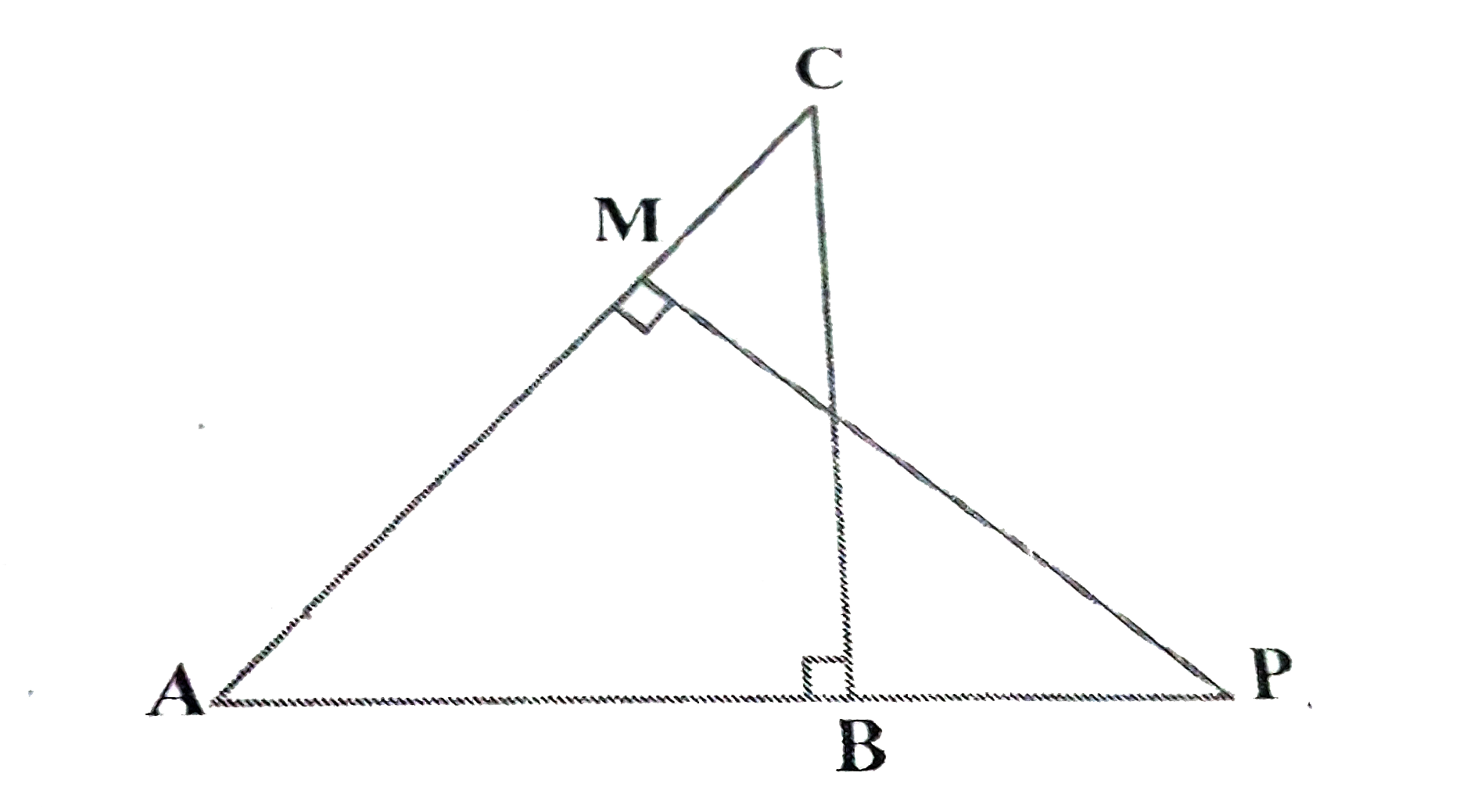
- In figure ABC and AMP are two right triangles, right angles at B and ...
Text Solution
|
- In figure ABC and AMP are two right triangles, right angles at B and ...
Text Solution
|
- In figure Cm and RN are respectively the medians of DeltaA B Cand De...
Text Solution
|
- Identify A, B. C and Din Figure 19.15 respectively. <img src="https:...
Text Solution
|
- Determine the point of symmetry of a regular hexagon. <img src="htt...
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- The inequation represented by the graph given below is : <img src="htt...
Text Solution
|