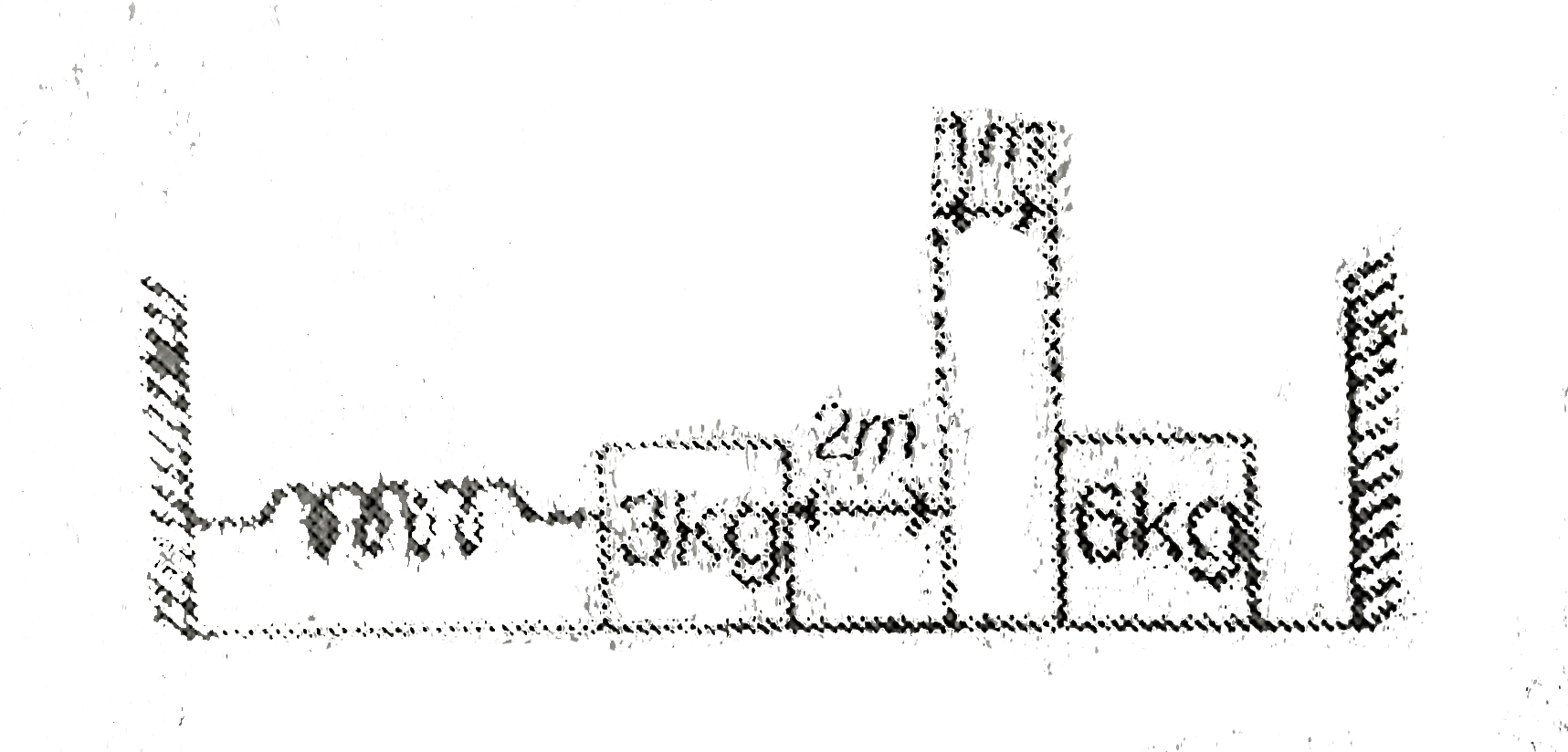A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SIMPLE HARMONIC MOTION
ALLEN|Exercise Exercise- 3 Match The Column|1 VideosSIMPLE HARMONIC MOTION
ALLEN|Exercise Asseration & Reason|7 VideosSIMPLE HARMONIC MOTION
ALLEN|Exercise Exercise-01|117 VideosRACE
ALLEN|Exercise Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)|25 VideosTEST PAPER
ALLEN|Exercise PHYSICS|4 Videos
Similar Questions
Explore conceptually related problems
ALLEN-SIMPLE HARMONIC MOTION-Exercise-02
- A mass M is performing linear simple harmonic motion. Then correct gra...
Text Solution
|
- A uniform cylinder of length (L) and mass (M) having cross sectional a...
Text Solution
|
- Two identical springs are fixed at one end and masses 1kg and 4kg are ...
Text Solution
|
- A cylindrical block of the density rho is partically immersed in a liw...
Text Solution
|
- A mass of 0.2 hg is attached to the lower end of a massles spring of f...
Text Solution
|
- A horizontal plank has a rectangular block placed on it. The plank sta...
Text Solution
|
- A particle is subjected to two simple harmonic motions along x and y d...
Text Solution
|
- A particle moves in the x-y the accoding to the equatio, r = (hati + 2...
Text Solution
|
- Two blocks A and B, each of mass m, are connected by a masslesss sprin...
Text Solution
|
- A solid uniform cylinder of mass M attached to a massless spring of fo...
Text Solution
|
- A ball is suspended by a thread of length l at the point O on an incl...
Text Solution
|
- A cage of mass M hangs from a light spring of force constant k. A body...
Text Solution
|
- In the above problem, the frequnecy of oscillations of the cage will b...
Text Solution
|
- The amplitude of a particle executing SHM about O is 10 cm. Then
Text Solution
|
- The angular frequency of a spring block system is omega(0). This syste...
Text Solution
|
- The x-coordinate of a particle moving on x-axis is given by x = 3 sin...
Text Solution
|
- Two blocks of masses 3 kg and 6kg rest on horizontal smooth surface. T...
Text Solution
|
- A disc of mass 3 m and a disc of mass m are connected by a massless sp...
Text Solution
|
- The displacement-time graph of a particle executing SHM is shown in fi...
Text Solution
|