A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
BITSAT GUIDE-MAGNETOSTATICS -BITSAT Archives
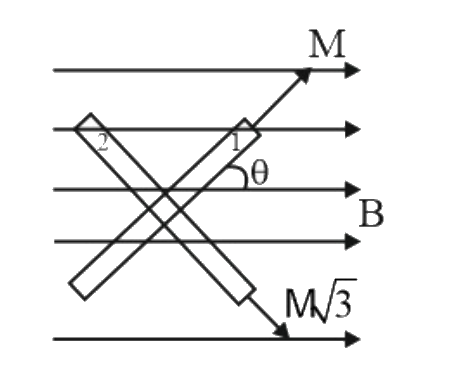
- Two short bar magnets of dipole moments M and Msqrt(3) are joined at r...
Text Solution
|
- The susceptibility of magnesium at 300 K is 1.2 xx 10^(-5). At what te...
Text Solution
|
- Magnetic moment of bar magnet is M. The work done to turn the magnet b...
Text Solution
|
- If m is magnetic moment and B is the magnetic field, then the torque i...
Text Solution
|
- At the magnetic north pole of the earth, the value of horizontal compo...
Text Solution
|
- With a standard rectangular bar magnet, the time period in the uniform...
Text Solution
|
- A magnetised wire of magnetic moment 'M' and length 'l' is bent in the...
Text Solution
|
- Susceptibility of ferromagnetic substance is
Text Solution
|
- Among the following properties describing diamagnetism, identify the ...
Text Solution
|