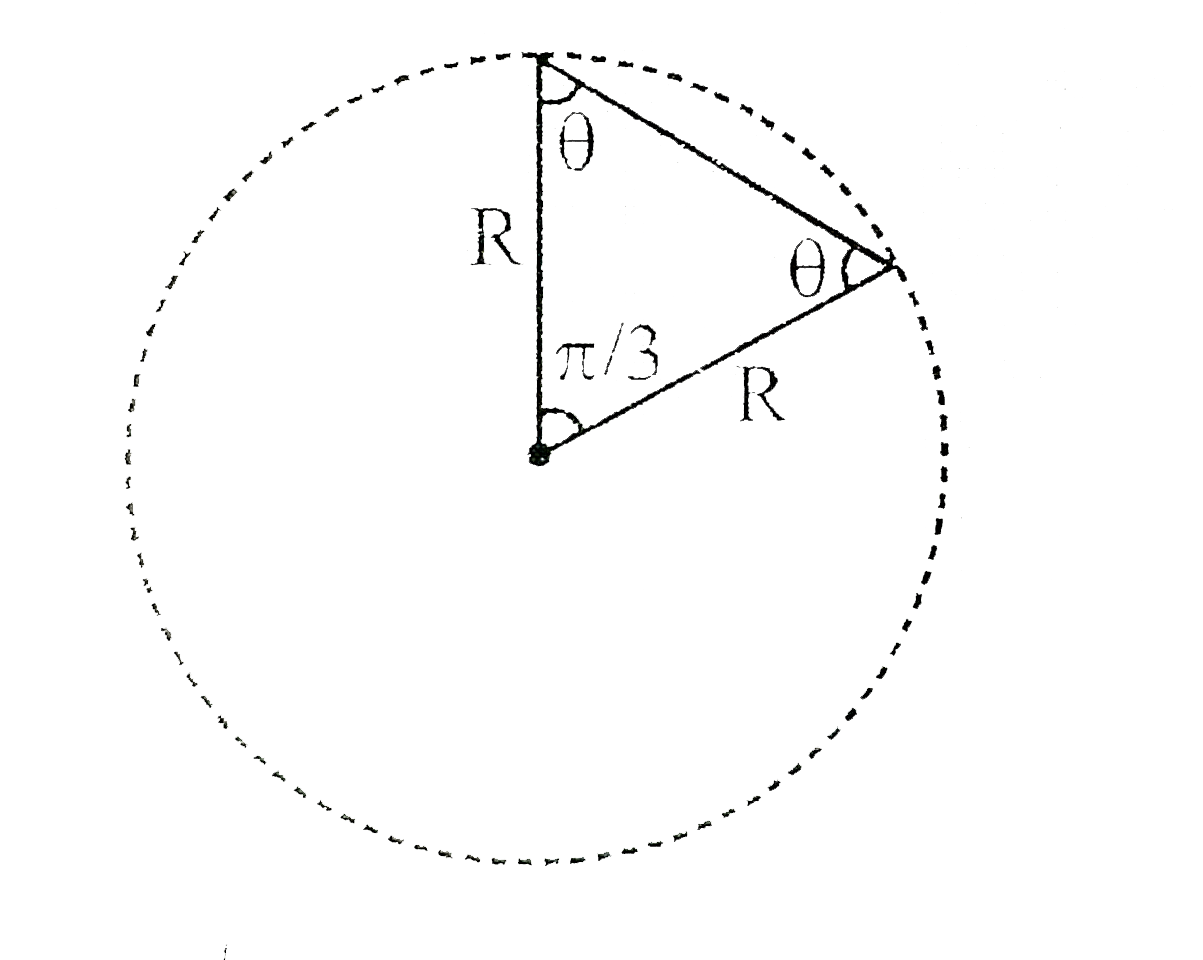Text Solution
Verified by Experts
The correct Answer is:
BANSAL-TEST PAPERS-PHYSICS PART (C )
- If the period 'T' of a drop under surface tension 's' is given by T =...
Text Solution
|
- A car starts from P and follows the path as shown in figure. Finally c...
Text Solution
|
- The dot product of 2 vectors is 10 unit and the magnitude of their res...
Text Solution
|
- If the position vector of a particle is given by vec(r ) = (cos 2t) ha...
Text Solution
|
- The mass m of the heaviest stone that can be moved by the water flowin...
Text Solution
|
- In a river flowing at 20 m//s, a swimmer who can swin at 10 m//s relat...
Text Solution
|
- A particle is projected vertically upwards from O with a velocity and ...
Text Solution
|
- A ball is projected at an angle 45^(@) as shown with speed 20 sqrt2 m/...
Text Solution
|
- The resultant of two velocity vectors vec(A) and vec(B) is perpendicul...
Text Solution
|
- The figure shown below is a system of two masses 3 kg and 6 kg and mas...
Text Solution
|
- A particle is moving in a circle of radious R with constant speed. The...
Text Solution
|
- In a river, a row boat is travelling down stram at a speed of 8 m/s wi...
Text Solution
|
- A damp washcloth is hung over the edge of a table to dry. Thus, part (...
Text Solution
|
- Two particles P and Q describe coplanar concentric circles of radii a ...
Text Solution
|
- A projectile is fired at speed v at an angle theta with horizontal. If...
Text Solution
|