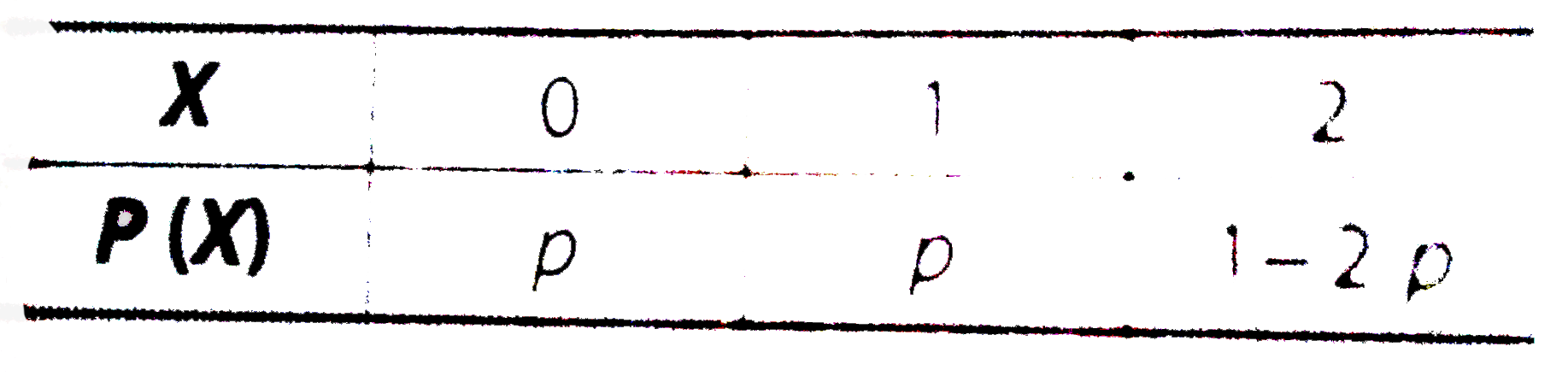Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR-PROBABILITY-Probability
- If two natural numbers r and s are drawn one at a time, without replac...
Text Solution
|
- Find the probability distribution of the maximum of two scores obtaine...
Text Solution
|
- The random variable X can take only the values 0,1,2. If P(X=0)=P(X=...
Text Solution
|
- Find the varience of the following distribution.
Text Solution
|
- A and B throw a pair of dice alternately. A wins the game, if he gets ...
Text Solution
|
- Two dice are tossed. Find whether the following two events A and B are...
Text Solution
|
- An urn contains m white and n black balls. A ball is drawn at random ...
Text Solution
|
- Three bags contain a number of red and white balls as follows Bag I : ...
Text Solution
|
- Refer to question 41 above. If a white ball is selected, what is the p...
Text Solution
|
- A shopkepper sells three types of flower seeds A(1),A(2) and A(3). The...
Text Solution
|
- A letter is known to have come either from 'TATA NAGAR or from 'CALCUT...
Text Solution
|
- There are two bags,one of which contains 3 black and 4 white balls whi...
Text Solution
|
- There are three urns containing 2 white and 3 black balls, 3 white and...
Text Solution
|
- By examining the chest X-ray, probability that T.B is detected when a ...
Text Solution
|
- An item is manufactured by three machines A, B and C. Out of the total...
Text Solution
|
- Let X be a discrete random variable whoose probability distribution is...
Text Solution
|
- The probability distribution of a discrete random variable x is given ...
Text Solution
|
- The probability distribution of a random variable x is given as under ...
Text Solution
|
- A bag contains (2n+1) coins. It is known that n of these coins have a ...
Text Solution
|
- Two cards are drawn successively without replacement from a well shuff...
Text Solution
|