Text Solution
Verified by Experts
Topper's Solved these Questions
CIRCLES
NAGEEN PRAKASHAN|Exercise Problems From NCERT/exemplar|11 VideosCIRCLES
NAGEEN PRAKASHAN|Exercise Exercise|25 VideosARITHMETIC PROGRESSION
NAGEEN PRAKASHAN|Exercise Revision Exercise Long Answer Question|5 VideosCO-ORDINATE GEOMETRY
NAGEEN PRAKASHAN|Exercise Revision Exercise Short Answer Questions|9 Videos
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN-CIRCLES-Revision Exercise Long Answer Questions
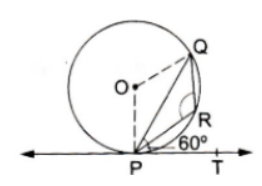
- In the adjoining figure, PQ is a chord of a circle and PT is the tange...
Text Solution
|
- In the given figure the sides AB, BE and CA of triangle ABC touch a c...
Text Solution
|
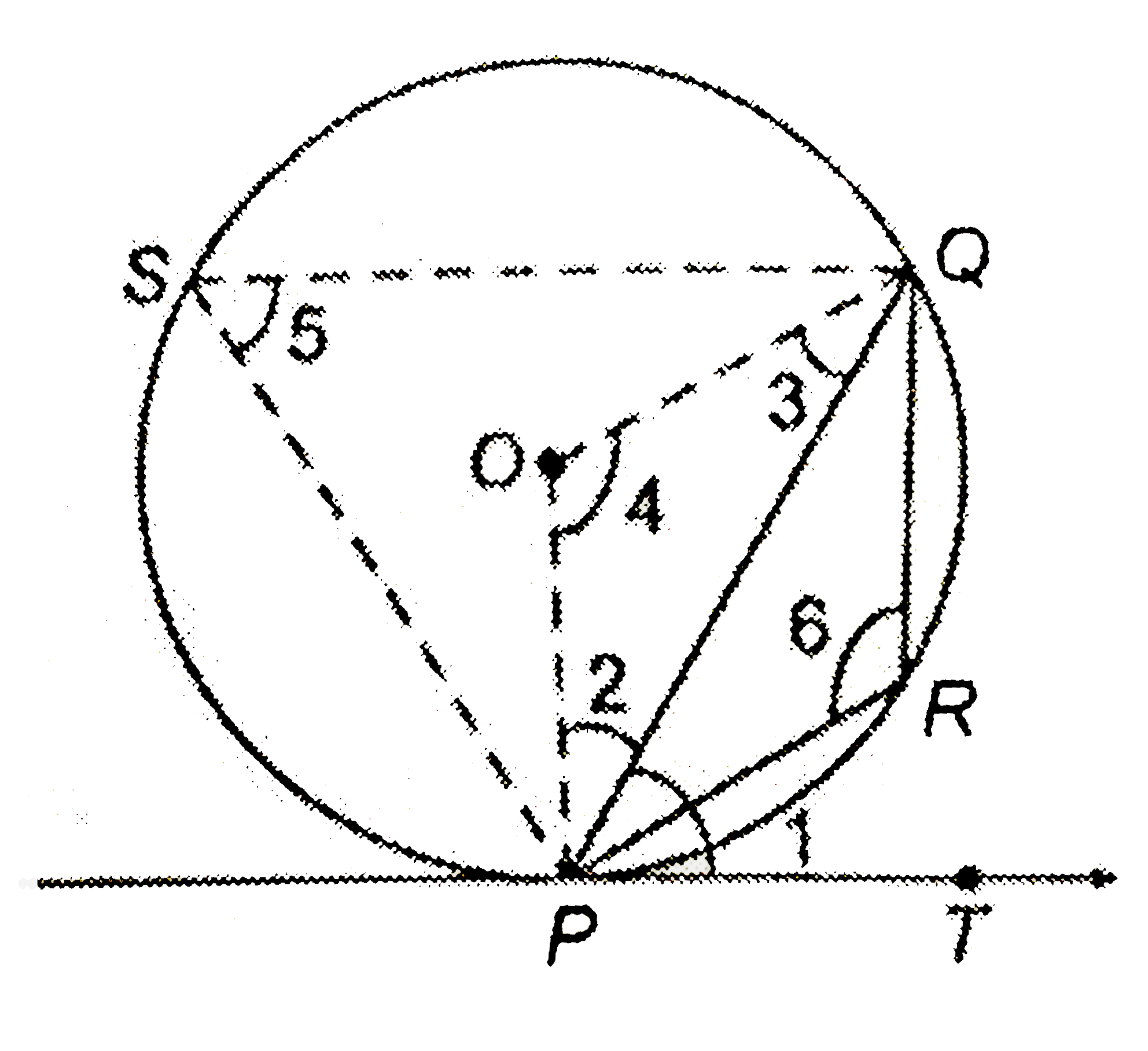
- Prove that the tangents at the extremities of any chord make equal ...
Text Solution
|
- Two tangents T P and T Q are drawn to a circle with centre O fro...
Text Solution
|