Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
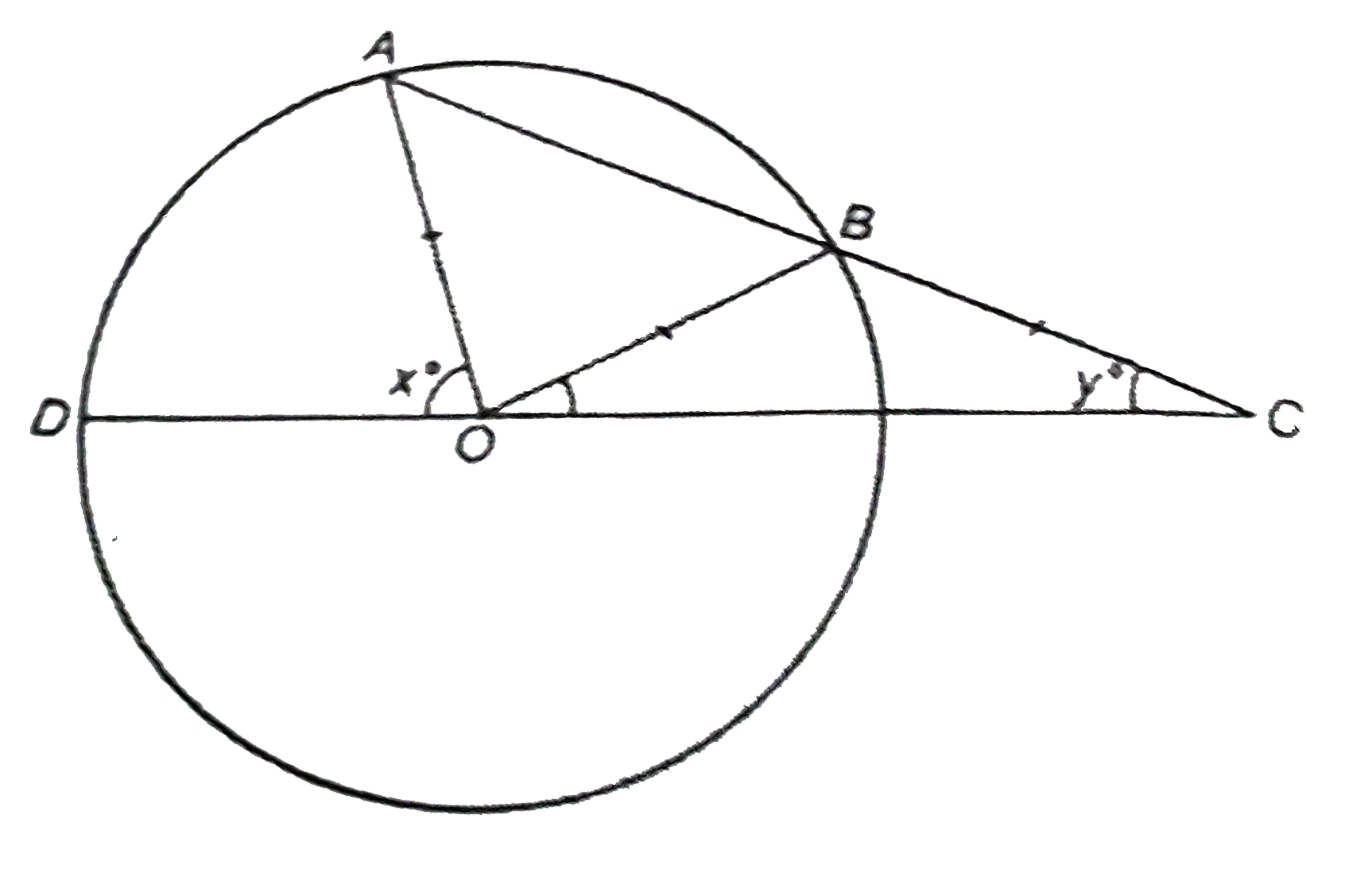
- AB is the chord of a circle with centreO. AB is produced to C, such th...
Text Solution
|
- AB and CD are equal chords of a circle whose centre is O,when produced...
Text Solution
|
- AB is the chord of a circle with centreO. AB is produced to C, such th...
Text Solution
|
- Two variable chords AB and BC of a circle x^(2)+y^(2)=a^(2) are such t...
Text Solution
|
- O केन्द्र के वृत्त की एक जीवा AB है | AB को C तक इस प्रकार बढ़ाया गया ह...
Text Solution
|
- In circle AOD is diameter with centre of circle O and AB, BC, CD are e...
Text Solution
|
- AB is a chord of a circle (centre o) and DOC is a line segment origina...
Text Solution
|
- In the given figure AB is the diameter and AC is the chord of a circle...
Text Solution
|
- AB is the diameter and AC is a chord of a circle with centre O such th...
Text Solution
|