A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
NCERT FINGERTIPS|Exercise Moment Of Inertia|7 VideosSYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
NCERT FINGERTIPS|Exercise Theorems Of Perpendicular And Parallel Axes|5 VideosSYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
NCERT FINGERTIPS|Exercise Torque And Angular Momentum|11 VideosPRACTICE PAPERS
NCERT FINGERTIPS|Exercise Practice Paper 3|50 VideosTHERMAL PROPERTIES OF MATTER
NCERT FINGERTIPS|Exercise Assertion And Reason|10 Videos
Similar Questions
Explore conceptually related problems
NCERT FINGERTIPS-SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS-Equilibrium Of A Rigid Body
- A rigid body is said to be in partial equilibrium, when it is in
Text Solution
|
- Moment of couple is called
Text Solution
|
- A couple produces.
Text Solution
|
- Which of the following statements is incorrect?
Text Solution
|
- Which of the following relations is correct?
Text Solution
|
- A rigid rod of length 2 L is acted upon by some forces. All forces lab...
Text Solution
|
- (1) Centre of gravity (C.G.) of a body is the point at which the weigh...
Text Solution
|
- A non-uniform bar of weight W and length L is suspended by two strings...
Text Solution
|
- A uniform rod of length 1 m mass 4 kg is supports on tow knife-edges p...
Text Solution
|
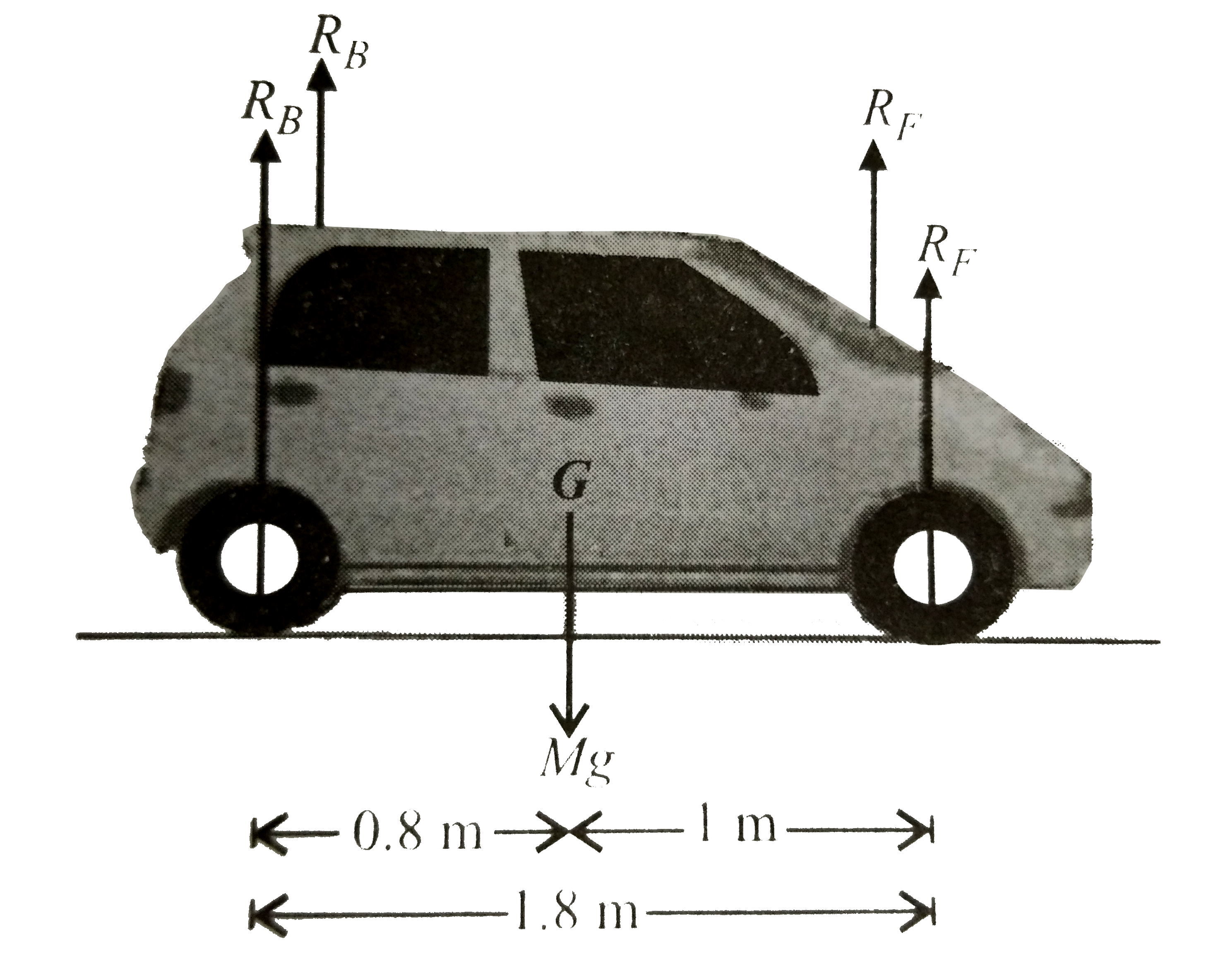
- A car weighs 1800 kg. The distance between its front and back axles is...
Text Solution
|
- A 3m along ladder weighing 20 kg leans on a frictionless wall. Its fee...
Text Solution
|
- A metre stick is balanced on a knife edge at its centre. When two coin...
Text Solution
|
- A uniform cube of mass m and side a is placed on a frictionless horizo...
Text Solution
|