Text Solution
Verified by Experts
Topper's Solved these Questions
KINEMATICS
FIITJEE|Exercise ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL-I (Short Answer Type Questions)|3 VideosKINEMATICS
FIITJEE|Exercise ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL-I (Fill in the Blanks:)|2 VideosKINEMATICS
FIITJEE|Exercise Comprehension|4 VideosHEAT AND TEMPERATURE
FIITJEE|Exercise NUMERICAL BASES QUESTIONS|1 VideosLAWS OF MOTION
FIITJEE|Exercise COMPREHENSION-III|2 Videos
Similar Questions
Explore conceptually related problems
FIITJEE-KINEMATICS-Exercise
- Referring to the previous illustration (a) What is the significance o...
Text Solution
|
- Which of the following graph is wrong?
Text Solution
|
- A car accelerates from rest with a =2 m//sec^(2) in a straight track, ...
Text Solution
|
- Referring to the previous illustration, what is the (a) acceleration ...
Text Solution
|
- Referring to the previous Nutrition, find the displacement-time equati...
Text Solution
|
- Find the average speed of a particle whose velocity is given by v=v si...
Text Solution
|
- Referring to the previous Illustration, if the stone reaches the groun...
Text Solution
|
- A body is released from a great height and falls freely towards the ea...
Text Solution
|
- Referring to the previous illustration (a) Where do the particles mee...
Text Solution
|
- Afrala moves due east with a velocity 20 m/s and a car moves due north...
Text Solution
|
- Roforning to previous illustration, what is the time or crossing mo ri...
Text Solution
|
- Referring to previous illustration, (a)if the width of tho giver is 0...
Text Solution
|
- Referring to previous wustration, what is the time elapsed for swimmin...
Text Solution
|
- Referring to the previous illustration, find the (a) what is the valu...
Text Solution
|
- Referring to the previous illustration, find the time of flight of the...
Text Solution
|
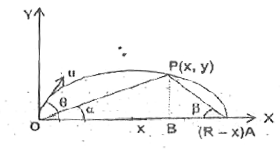
- A particle is thrown over a triangle from one end of a horizontal base...
Text Solution
|
- Referring to the previous illustration, if the boy releases the ball f...
Text Solution
|
- Referring to the provious illustration, if the maximum heights for two...
Text Solution
|
- A ball starts falling with zero initial velocity on a smooth inclined ...
Text Solution
|
- Find the total acceleration of a particle, moving in a circular track ...
Text Solution
|