Text Solution
Verified by Experts
Topper's Solved these Questions
WORK, ENERGY AND POWER
FIITJEE|Exercise ASSIGNMENT PROBLEMS ( SUBJECTIVE) (LEVEL-I) Short Answer Type Question|2 VideosWORK, ENERGY AND POWER
FIITJEE|Exercise ASSIGNMENT PROBLEMS ( SUBJECTIVE) (LEVEL-I) Fill in the blank|2 VideosWORK, ENERGY AND POWER
FIITJEE|Exercise MATRIX MATCH TYPE|6 VideosTEST PAPERS
FIITJEE|Exercise PHYSICS|747 Videos
Similar Questions
Explore conceptually related problems
FIITJEE-WORK, ENERGY AND POWER -Exercise
- A tug, exerting a pulling force of 800 N due north, tows a barge throu...
Text Solution
|
- (a) A particle is acted upon by a force vec(F) given by vec(F)=A cos o...
Text Solution
|
- A man in an open car moving with high speed, throws a ball his full ca...
Text Solution
|
- Is work done by a non conservative force always negative ? Comment.
Text Solution
|
- Can a body have momentum when its energy it negative?
Text Solution
|
- Find the work done by an external agent in lowering a block of mass m ...
Text Solution
|
- Two springs have force constants k(1) " and " k(2) (k(1) gt k(2)). On ...
Text Solution
|
- If the momentum of a body is increased by 50%, then the percentage inc...
Text Solution
|
- A lorry and a car moving with the same kinetic energy are brought to r...
Text Solution
|
- A block of mass m = 0.1 kg is released from a height of 4 m on a curve...
Text Solution
|
- When you lift a box from the floor and put it one an almirah the ptote...
Text Solution
|
- When you push your bicycle up on an incline the potential energy of th...
Text Solution
|
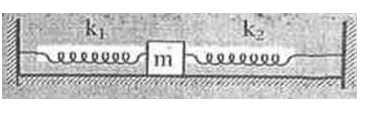
- A block of mass m is attached to two unstretched springs of spring con...
Text Solution
|
- A plate of mass m, length b, and breadth a is initially lying on a hor...
Text Solution
|
- A spring, placed horizontally on a rough surface is compressed by a bl...
Text Solution
|
- (i) Two bodies of masses m(1)(m(2) gt m(1)) are connected by a light i...
Text Solution
|