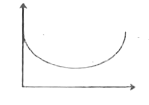
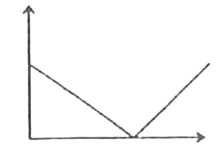
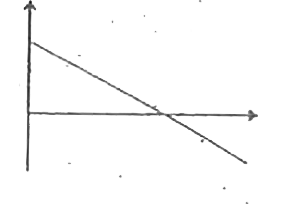
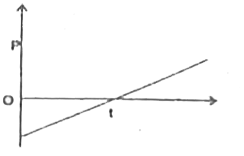
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
WORK, ENERGY AND POWER
FIITJEE|Exercise ASSIGNMENT PROBLEMS ( OBJECTIVE) (LEVEL-I) (ASSERTION REASONING TYPE)|2 VideosWORK, ENERGY AND POWER
FIITJEE|Exercise ASSIGNMENT PROBLEMS ( OBJECTIVE) (LEVEL-II)|19 VideosWORK, ENERGY AND POWER
FIITJEE|Exercise ASSIGNMENT PROBLEMS ( SUBJECTIVE) (LEVEL-II & III)|15 VideosTEST PAPERS
FIITJEE|Exercise PHYSICS|747 Videos
Similar Questions
Explore conceptually related problems
FIITJEE-WORK, ENERGY AND POWER -ASSIGNMENT PROBLEMS ( OBJECTIVE) (LEVEL-I)
- A small body slides from rest along two equally rough circular surface...
Text Solution
|
- In an XY horizontal plane a force field vecF=-(40N//m)(yhati+xhatj) is...
Text Solution
|
- A stone is projected at time t=0 with a speed v(0) at an angle theta ...
Text Solution
|
- A block of mass m is suspended by a light thread from an elevator. The...
Text Solution
|
- A particle initially at rest is displaced from x=-10 m to x=+10m, und...
Text Solution
|
- A particle of mass m starts from rest and moves in a circular path of ...
Text Solution
|
- A particle of mass m attached to an inextensible light string is mov...
Text Solution
|
- A block of mass 10 kg accelerates uniformly from rest to a speed of 2 ...
Text Solution
|
- A conservative force acts on a particle as the particle moves along ...
Text Solution
|
- A particle moves along the X-axis from x=0 to x=5m under the influence...
Text Solution
|
- Two springs have their force constant as K(1) and K(2)(K(1)lt K(2)). W...
Text Solution
|
- A body of mass 0.1 g moving with a velocity of 10 m/s hits a spring (f...
Text Solution
|
- A body of mass 1 kg thrown with a velocity of 10m/s comes to rest ( mo...
Text Solution
|
- A fixed wedge ABC is in the shape of an equilateral triangle of side l...
Text Solution
|
- One fourth chain is hanging down from a table work done to bring the h...
Text Solution
|
- A force shown in the F-x graph is applied to 5 kg cart, which then coa...
Text Solution
|
- A body of mass 100 g is rotating in a circular path of radius r with...
Text Solution
|
- What is the velocity of the bob of a simple pendulum at its mean posit...
Text Solution
|
- A car moving with a velocity of 10m/s can be stopped by the applicatio...
Text Solution
|
- A block of mass m = 0.1 kg is released from a height of 4 m on a curve...
Text Solution
|