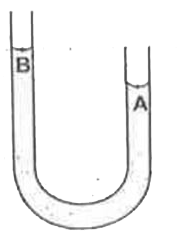
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
FIITJEE-FLUID MECHANICS -NUMERICAL BASED QUESTIONS
- A circular ring of small thickness and of inner and outer diameters...
Text Solution
|
- A small ball of volume V and density rho is held inside a cubical co...
Text Solution
|
- If n identical water droplets falling under gravity with terminal vel...
Text Solution
|
- The difference in water levels in the two communicating capillary tu...
Text Solution
|