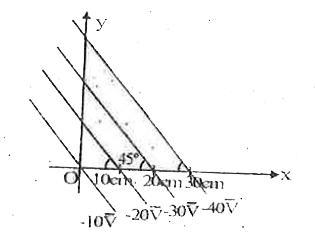
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
GRAVITATION
FIITJEE|Exercise Assertion & Reasoning type|1 VideosGRAVITATION
FIITJEE|Exercise Numerical based Questions|4 VideosGRAVITATION
FIITJEE|Exercise Solved problem (Objective)|15 VideosGMP ASSESMENT
FIITJEE|Exercise Numerical Based|61 VideosHEAT AND TEMPERATURE
FIITJEE|Exercise NUMERICAL BASES QUESTIONS|1 Videos
Similar Questions
Explore conceptually related problems
FIITJEE-GRAVITATION-Comprehension
- The orbit of geostationary satelite is circular , the time period of s...
Text Solution
|
- Three particles, each of mass m are fixed at the vertices of an equila...
Text Solution
|
- Three particles, each of mass m are fixed at the vertices of an equila...
Text Solution
|
- Gravitational force is a conservation and medium independent force. It...
Text Solution
|
- Gravitational force is a conservation and medium independent force. It...
Text Solution
|
- Gravitational force is a conservation and medium independent force. It...
Text Solution
|
- The gravitational field strength vecE and gravitational potential V ar...
Text Solution
|
- The gravitational field strength vecE and gravitational potential V ar...
Text Solution
|
- The gravitational field strength vecE and gravitational potential V ar...
Text Solution
|
- The motion of a planet around sun in an elliptical orbit is shown in t...
Text Solution
|
- The motion of a planet around sun in an elliptical orbit is shown in t...
Text Solution
|
- The gravitational field strength vecE and gravitational potential V ar...
Text Solution
|
- The gravitational field strength vecE and gravitational potential V ar...
Text Solution
|