Similar Questions
Explore conceptually related problems
Recommended Questions
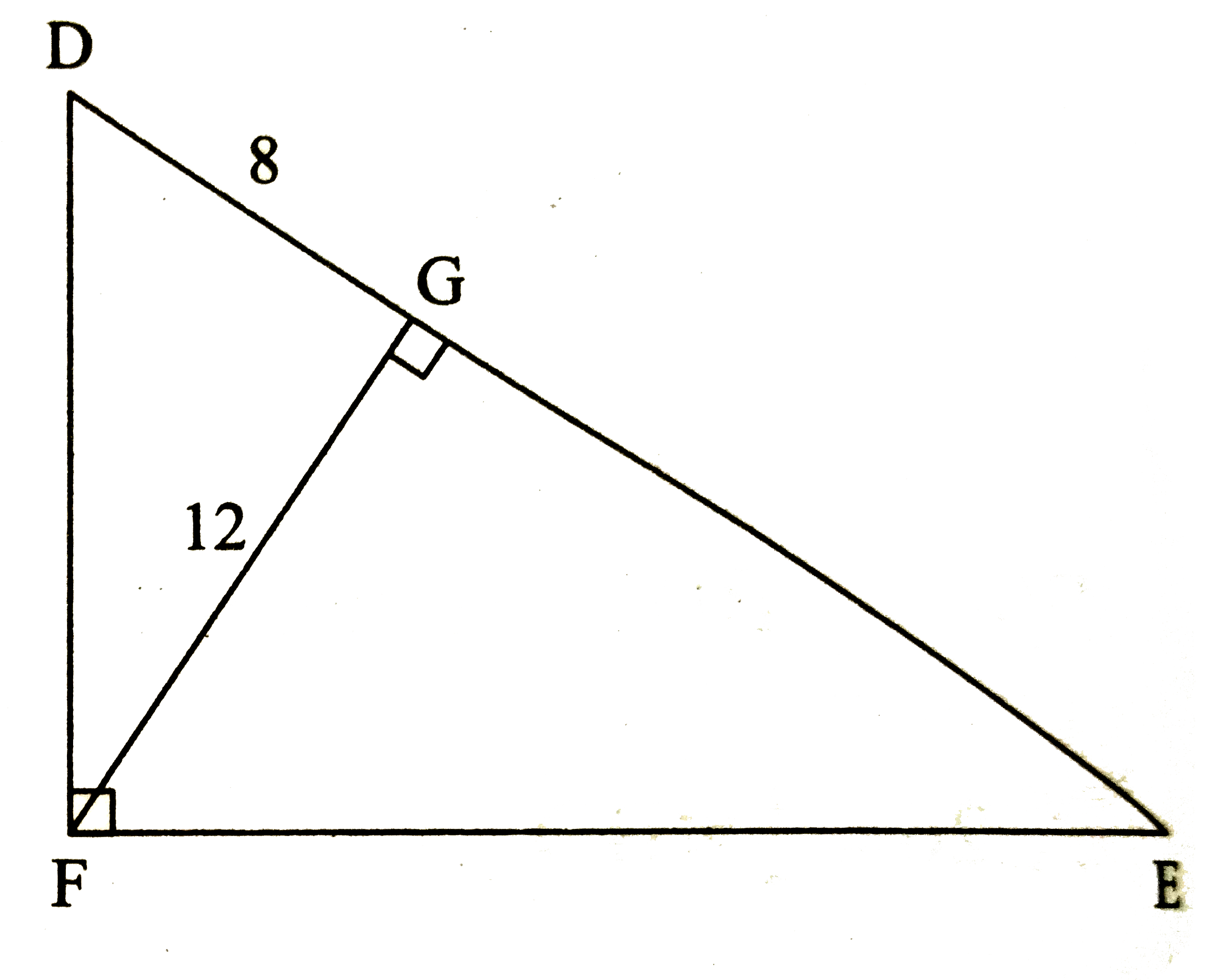
- In the figure, /DFE=90^(@), seg FG bot side DE, DG=8, FG=12 then compl...
Text Solution
|
- The value of |[a,a+d,a+2d] , [a+d,a+2d,a+3d] , [a+2d,a+3d,a+4d]|+|[b,b...
Text Solution
|
- Amongst the species Br^(-), Br, Br^(+), the smallest one in size is .
Text Solution
|
- In CH(3)CH(2)Br,% of Br is
Text Solution
|
- In the figure, /DFE=90^(@), seg FG bot side DE, DG=8, FG=12 then compl...
Text Solution
|
- In the figure, /LMN=/LKN=90^(@) seg MK bot seg LN. Complete the f...
Text Solution
|
- In DeltaABC,angleACB=90^(@) seg CD bot seg AB seg DE bot seg C...
Text Solution
|
- The correct order of size among Br^(+), Br, Br^(-)
Text Solution
|
- In the adjoining figure, angle DFE = 90^(@), FG bot ED if GD = 8, FG =...
Text Solution
|