लिखित उत्तर
Verified by Experts
The correct Answer is:
टॉपर्स ने हल किए ये सवाल
परवलय
JEE Main & Advanced (Hindi Medium)|Exercise एकल पूर्णांक प्रश्न|5 Videosपरवलय
JEE Main & Advanced (Hindi Medium)|Exercise दृढ़कथन-कारण प्रकार|2 Videosनिश्चित समाकलन
JEE Main & Advanced (Hindi Medium)|Exercise एकल पूर्णाक प्रश्न|7 Videosप्रतिलोम वृत्तीय फलन
JEE Main & Advanced (Hindi Medium)|Exercise एकल पूर्णांक प्रश्न|1 Videos
JEE Main & Advanced (Hindi Medium)-परवलय-विश्लेषणात्मक प्रश्न
- माना परवलय Y^(2)=4x के तीन भिन्न बिन्दुओं पर खींचे गए अभिलम्ब, बिन्दु ...
Text Solution
|
- परवलय y=x^(2) से बिन्दु (0,c), जहाँ 0 le c le 5 की निम्नतम दूरी ज्ञात ...
Text Solution
|
- वक्र x^2= 4y के उस अभिलम्ब का समीकरण ज्ञात कीजिए, जो बिन्दु (1, 2) से ...
Text Solution
|
- बिन्दु (c, 0) से वक्र y^(2)=x पर तीन अभिलम्ब खींचे जाते हैं। दिखाइए कि...
Text Solution
|
- परवलय y^(2)=4x के शीर्ष O से दो जीवायें OP और OQ खींची जाती हैं, जो एक...
Text Solution
|
- दिखाइए कि परवलय y^(2)=4ax की, प्रवणता 2 वाली जीवा को आन्तरिक रूप से 1:...
Text Solution
|
- बिन्दु A, B और C, परवलय y^(2)=4ax पर स्थित हैं। बिन्दु A, B और C पर खी...
Text Solution
|
- वृत्त x^(2)+y^(2)=2a^(2) तथा परवलय y^(2)=8ax की दो उभयनिष्ठ स्पर्श रेख...
Text Solution
|
- बिन्दु P से परवलय y^(2)=4ax पर खींचे गए स्पर्शी युग्म के बीच 45^@ का क...
Text Solution
|
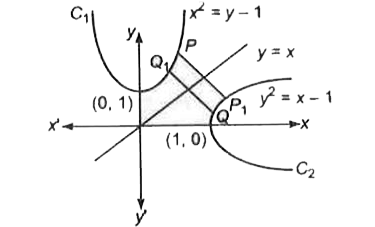
- माना C1" व "C2 क्रमश: परवलय x^(2)=y-1" और "y^(2)=x-1 हैं। माना P,C1" प...
Text Solution
|
- बिंदु P से परवलय y^(2)=4x" पर "m(1),m(2), m(3) प्रवणता के अभिलम्ब खींच...
Text Solution
|
- परवलय y^(2)-2y-4x+5=0 पर स्थित P बिन्दु पर एक स्पर्श रेखा खींची जाती ह...
Text Solution
|