Similar Questions
Explore conceptually related problems
Recommended Questions
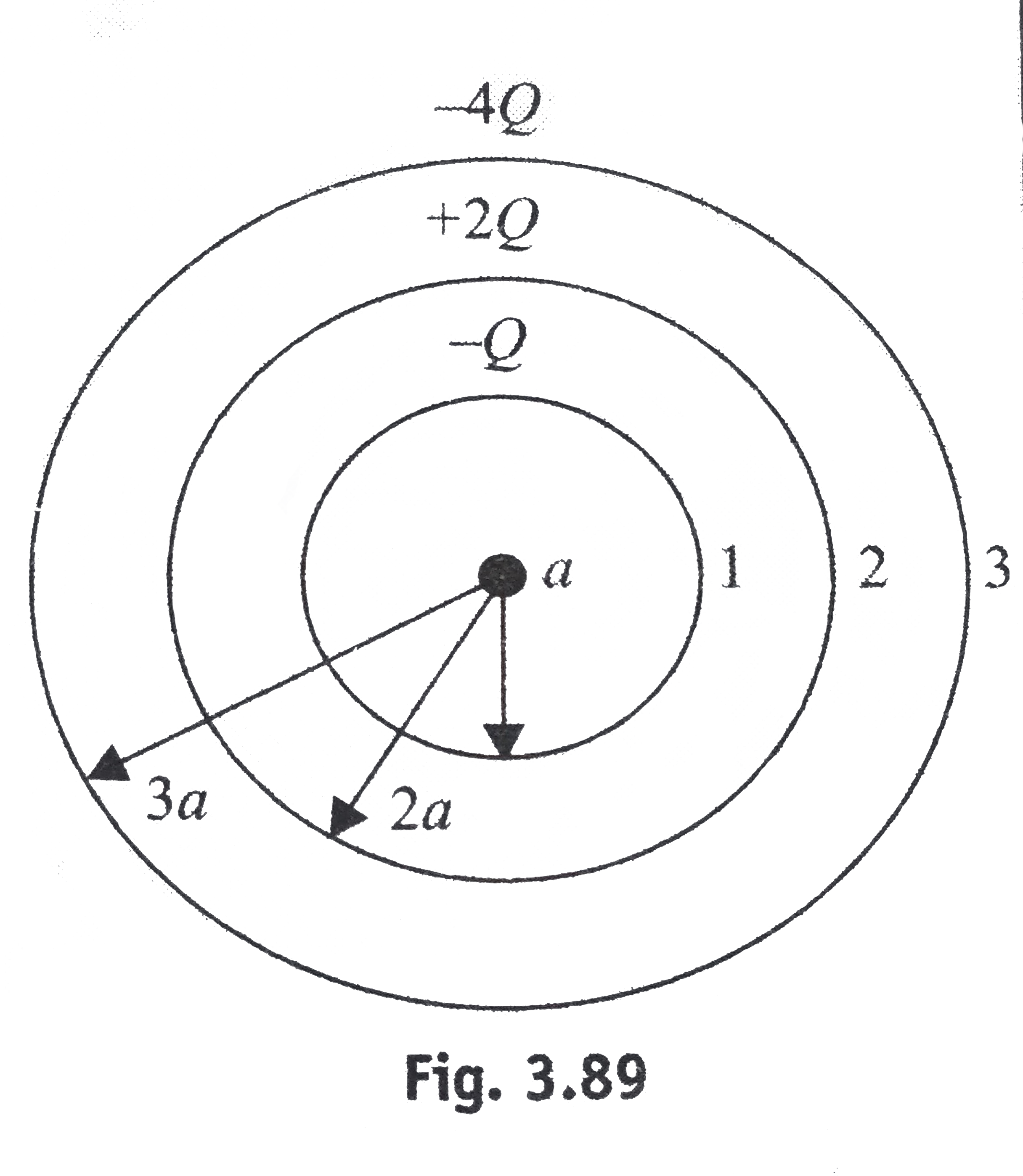
- Three concentric spherical conductors of radii a, 2a, and 3a have char...
Text Solution
|
- Three concentric spherical conductors of radii a, 2a, and 3a have char...
Text Solution
|
- A sphere of radius R contains charge density rho(r )=A (R-r ) , for 0 ...
Text Solution
|
- A sphere of radius R contains charge density rho(r )=A (R-r ) , for 0 ...
Text Solution
|
- Figure shown a section through two long thin concentric cylinders of r...
Text Solution
|
- If the potential at the center of a uniformly charged sphere of radius...
Text Solution
|
- एक ठोस धात्वीय गोले पर आवेश + 3Q है। इस गोले से संकेन्द्रीय एक चालक गो...
Text Solution
|
- O is the centre of two coplanar concentric circular conductors, A and ...
Text Solution
|
- A point charge +q is held at a distance R from the centre of an unchar...
Text Solution
|
 .
.