Similar Questions
Explore conceptually related problems
Recommended Questions
- A spherical ball of the radius R is made by joining two hemispherical ...
Text Solution
|
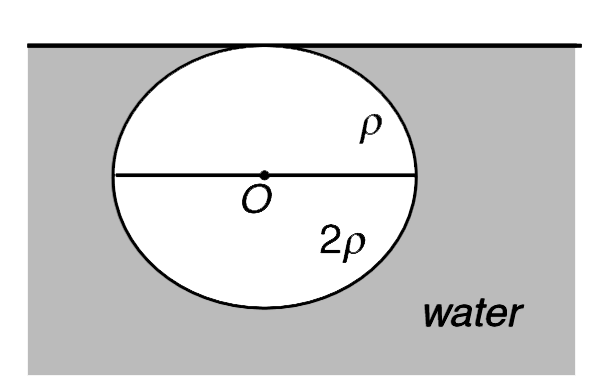
- A ball is made of a material of density rho where rho(oil)ltrholtrho(w...
Text Solution
|
- A small ball of mass m and density rho is dropped in a viscous liquid ...
Text Solution
|
- A spherical ball of radius R is floating at the interface of two liqui...
Text Solution
|
- A spherical ball of radius R is floating at the interface of two liqui...
Text Solution
|
- A sperical ball of radius r and relative density 0.5 is floating in eq...
Text Solution
|
- A spherical ball of the radius R is made by joining two hemispherical ...
Text Solution
|
- A ball is made of a material of density rho where rho("oil")ltrholt rh...
Text Solution
|
- घनत्व rho की एक गेंद है ( जहाँ पर rho("तेल")lt rho lt rho("जल")) | ते...
Text Solution
|