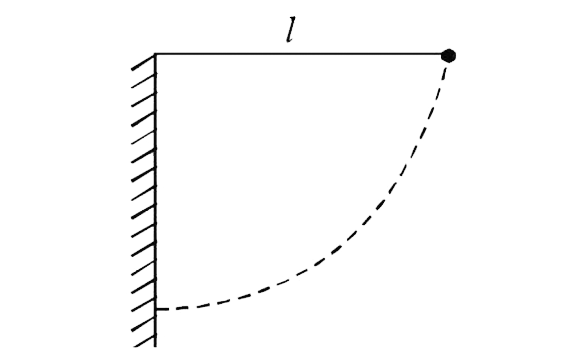Similar Questions
Explore conceptually related problems
Recommended Questions
- A simple pendalum is suspended from a peg on a verticle wall . The pen...
Text Solution
|
- A simple pendalum is suspended from a peg on a verticle wall . The pen...
Text Solution
|
- A simple pendulum is hanging from a peginserted in a vertical wall. It...
Text Solution
|
- A simple pendulum is suspended from a peg on a wall which is inclined ...
Text Solution
|
- A simple pendulum is hanging from a peg inserted in a vertical wall. I...
Text Solution
|
- The figure shows a pendulum of length l suspended at a distance x vert...
Text Solution
|
- A simple pendulum is supended from a peg on a verticl wall. The pendul...
Text Solution
|
- A pendulum bob on a 2 m string is displaced 60^(@) from the verticle a...
Text Solution
|
- A ladder 5 m long is leaning against a well. The bottom of the ladder ...
Text Solution
|