Similar Questions
Explore conceptually related problems
Recommended Questions
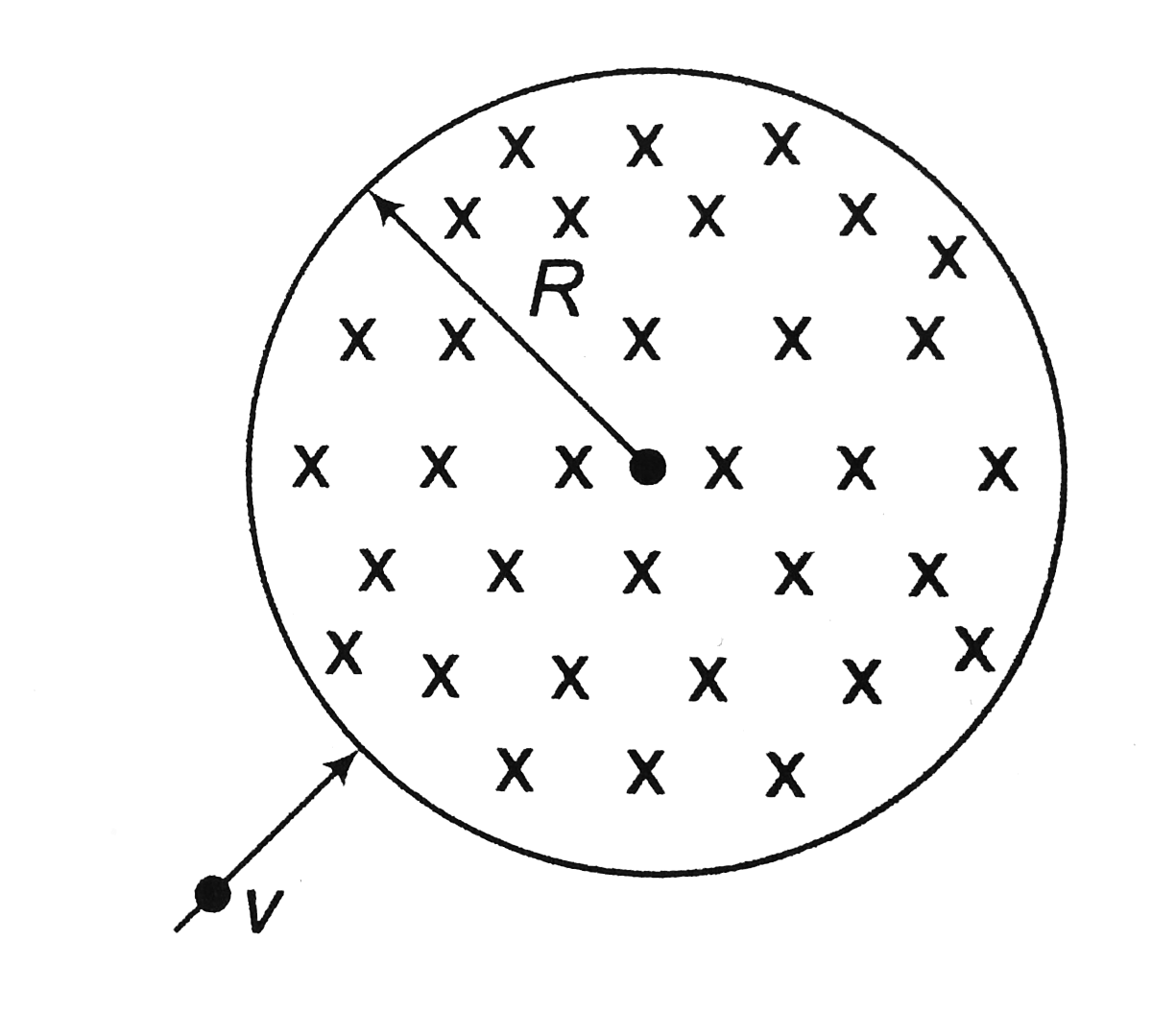
- A particle of mass m having a charge q enters into a circular region o...
Text Solution
|
- A charged particle of mass m and charge q is accelerated through a pot...
Text Solution
|
- A particle of mass m having a charge q enters into a circular region o...
Text Solution
|
- A charged particle of mass m and charge q is accelerated through a pot...
Text Solution
|
- A charged particle of mass m and charge q enters a magnetic field B wi...
Text Solution
|
- A particle of mass m and charge q enters a magnetic field B perpendicu...
Text Solution
|
- m द्रव्यमान का कण जिस पर आवेश q है, एकसमान चुम्बकीय क्षेत्र B के लम्ब...
Text Solution
|
- If a charge particle of charge q , mass m , moves in a circular path i...
Text Solution
|
- द्रव्यमान m एवं आवेश q का एक आवेशित कण एकसमान चुम्बकीय क्षेत्र B में त...
Text Solution
|