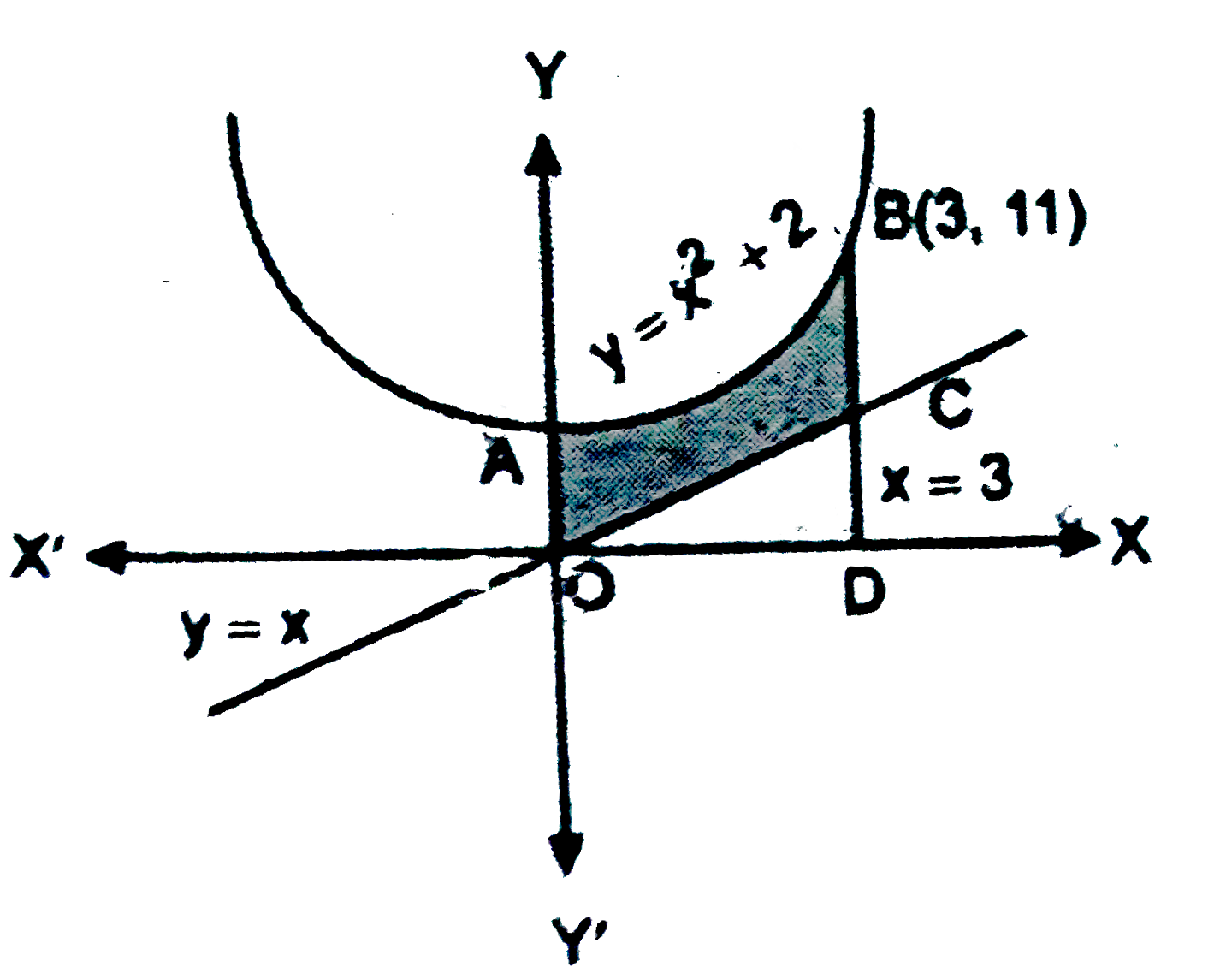Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Find the area of the region bounded by the curves y=x^2+2y=x ,x=0,a n ...
Text Solution
|
- Find the area of the region bounded by the curves x=2y-y^2 and y=2+x.
Text Solution
|
- Find the area of the region bounded by the curves 2y^2=x, 3y^2=x+1, y=...
Text Solution
|
- the area of region bounded by curves y^(2)=x and y=(x)/(3) is
Text Solution
|
- Find the area of the region bounded by the curve y=x^(3),y=x+6" and "x...
Text Solution
|
- वक्रों y=x^(2)+2, y=x, x=0 एवं x=3 से घिरे क्षेत्र का क्षेत्रफल ज्ञात ...
Text Solution
|
- वक्रो y = sqrtx, 2y - x + 3 = 0 तथा x अक्ष से घिरे उस क्षे...
Text Solution
|
- वक्रो y =x^(2) + 2,y=x ,x =0 एव x = 3 से घिरे क्षेत्र का क्षेत्रफ...
Text Solution
|
- वक्रों y=-1,y=2,x=y^(3) और x = 0 से घिरे क्षेत्र का क्षेत्रफल ज्ञात की...
Text Solution
|