If `i_(1) = 3 sin omega t ` and `i_(2) =6 cos omega t `, then `i_(3) ` is

If i_(1)=3 sin omega t and (i_2) = 4 cos omega t, then (i_3) is

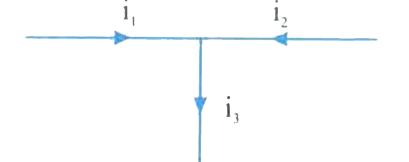
In the given figure, if i_(1)=3 sin omegat and i_(2)=4 cos t, then i_(3) is

Two wave are represented by equation y_(1) = a sin omega t and y_(2) = a cos omega t the first wave :-

The ratio of amplitudes of following SHM is x_(1) = A sin omega t and x_(2) = A sin omega t + A cos omega t

If i_(1) = i_(0) sin (omega t), i_(2) = i_(0_(2)) sin (omega t + phi) , then i_(3) =

x_(1) = 3 "sin" omega t , x_(2) = 4 "cos' omega t Find (i) amplitude of resultant SHM. (ii) equation of the resultant SHM.

x_(1) = 3 sin omega t implies x_(2) = 4 cos omega t . Find (i) amplitude of resultant SHm, (ii) equation of the resultant SHm.

The resultant amplitude due to superposition of three simple harmonic motions x_(1) = 3sin omega t , x_(2) = 5sin (omega t + 37^(@)) and x_(3) = - 15cos omega t is

x_(1) = 3 sin omega t ,x_(2) = 4 cos omega t Find (i) amplitude of resultant SHM, (ii) equation of the resultant SHM.