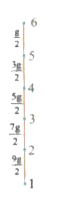
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A person sitting on the top of a tall building is dropping balls at re...
Text Solution
|
- A person sitting on the top of a tall building is dropping balls at re...
Text Solution
|
- four balls are dropped from the top of a tower at intervals of one - ...
Text Solution
|
- एक ऊँची ईमारत पर बैठा मनुष्य हर 1 सेकंड बाद एक गेंद गिरने ...
Text Solution
|
- Take two balls of different masses, go to the top of a building, drop ...
Text Solution
|
- The distance ,d, in feet covered by a ball in the n^(th) second aft...
Text Solution
|
- A ball is dropped downward from the roof of a building and simultaneou...
Text Solution
|
- A ball is dropped downward from the roof of a building and simultaneou...
Text Solution
|
- A ball is dropped from the top of a building. The ball takes 0.5 s to ...
Text Solution
|