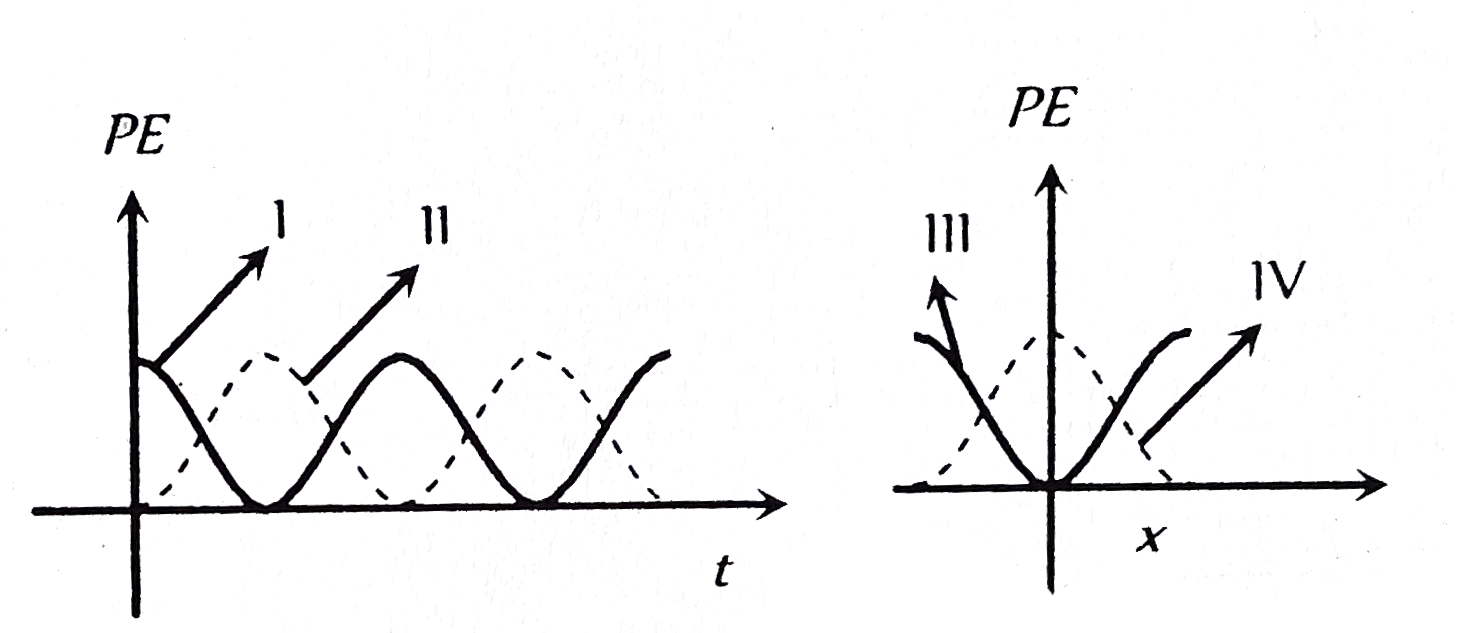For a particle executing S.H.M. the disp...

For a particle executing S.H.M. the displacement x is given by ` x= A cos omegat` . Identify the graph which represents the variation of potential energy (P.E.) as a function of time

I, III

II, IV

II, III

I, IV

Text Solution

Verified by Experts

The correct Answer is:

Topper's Solved these Questions

OSCILLATIONS
NARAYNA|Exercise EXERCISE - III|29 Videos
OSCILLATIONS
NARAYNA|Exercise EXERCISE - IV|41 Videos
OSCILLATIONS
NARAYNA|Exercise EXERCISE - II (C.W)|27 Videos
NEWTONS LAWS OF MOTION
NARAYNA|Exercise PASSAGE TYPE QUESTION|6 Videos
PHYSICAL WORLD
NARAYNA|Exercise C.U.Q|10 Videos

Similar Questions

Explore conceptually related problems

For a particle executing SHM, the displacement x is given by x = A cos omegat . Identify the graph which represents the variation of potential energy (PE) as a function of time t and displacement x . (a) I, III (b) II, IV (c ) II, III (d) I, IV

For a particle executing simple harmonic motion, the displacement x is given by x= Acosomegat . Identify the graph, which represents the variation of potential energy (U) as a function of time t and displacement x.

If for a particle executing SHM, the equation of SHM is given as y=acosomegat . Then which of the following graphs represents the variation in potential energy?

For a particle executing SHM , the kinetic energy (K) is given by K = K_(0)cos^(2) omegat . The equation for its displacement is

The displacement of a particle is given by x = cos^(2) omegat. The motion is

For a particle executing S.H.M., the kinetic energy K is given K = K_(0) cos ^(2)omega t . The maximum value of potential energy is:

The displacement of a particle executing a S.H.M. is given by x= A "sin" omega t +A "cos" omega t . What is the amplitude of motion ?

Which of the following graphs best represents the variation of acceleration 'a' with displacement x?

Draw the graph between displacement and potential energy for a particle executing SHM.

NARAYNA-OSCILLATIONS-EXERCISE - II (H.W)

A particle of mass m is released from rest and follow a particle part ...
Text Solution
|
A particle of mass m is allowed to oscillate near the minimum of a ver...
Text Solution
|
{:("List - I","List - II"),("(a) Planets revolving around the sun","(e...
Text Solution
|
The acceleration a of a particle undergoing S.H.M. is shown in the fig...
Text Solution
|
Graph between velocity and displacement of a particle, executing S.H.M...
Text Solution
|
A particle is placed at the origin and a force F=Kx is acting on it (w...
Text Solution
|
The velocity-time graph of a particle executing SHM is as shown in the...
Text Solution
|
The smallest time interval between maximum and minimum velocities of t...
Text Solution
|
The acceleration-displacement graph of a particle executing SHM is as ...
Text Solution
|
The acceleration-displacement graph of two particles P and Q exeucting...
Text Solution
|
A simple harmonic oscillator starts from mean position at time, t = 0,...
Text Solution
|
For a particle executing SHM, if x, v, a and F represent dispacement, ...
Text Solution
|
A second pendulum is shifted from a plane where g = 9.8 m//s^(2) to an...
Text Solution
|
A simple pendulum with a brass bob has a period T. The bob is now imme...
Text Solution
|
Calculate the time period of a simple pendulum whose length is equal t...
Text Solution
|
The l - T^(2) graph of a simple pendulum is an shown in the figure. Th...
Text Solution
|
l - T and l-T^(2) graphs of a simple pendulum on earth are as shown in...
Text Solution
|
For a particle executing S.H.M. the displacement x is given by x= A c...
Text Solution
|
The variation of potential energy (U) of a simple harmonic oscillator ...
Text Solution
|