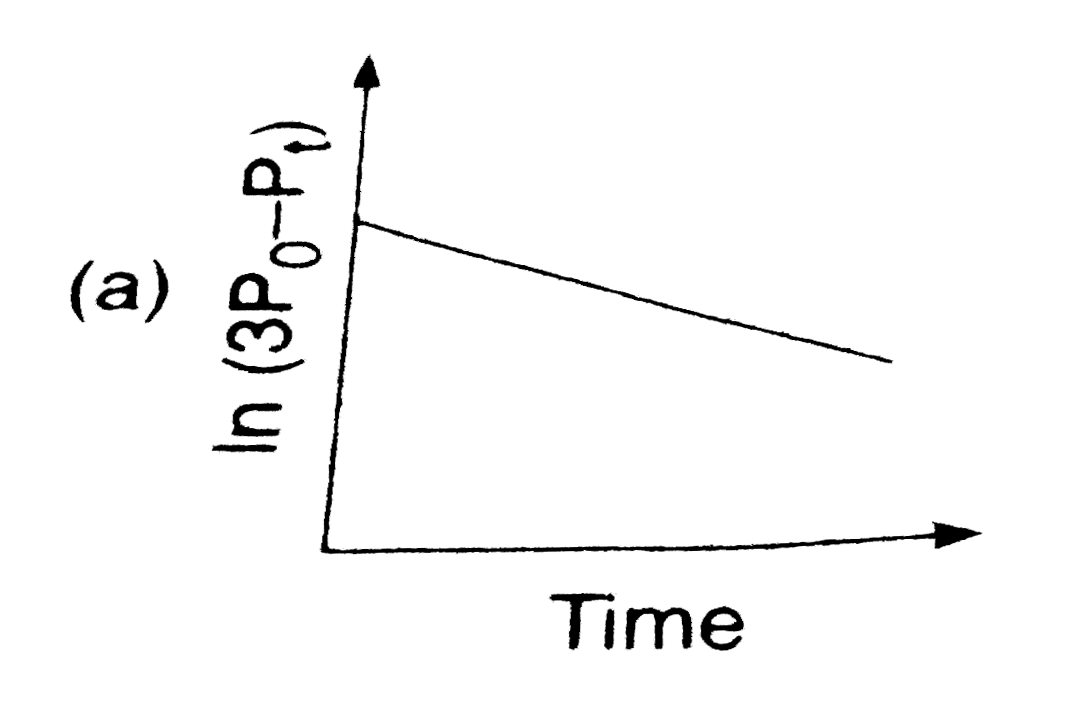
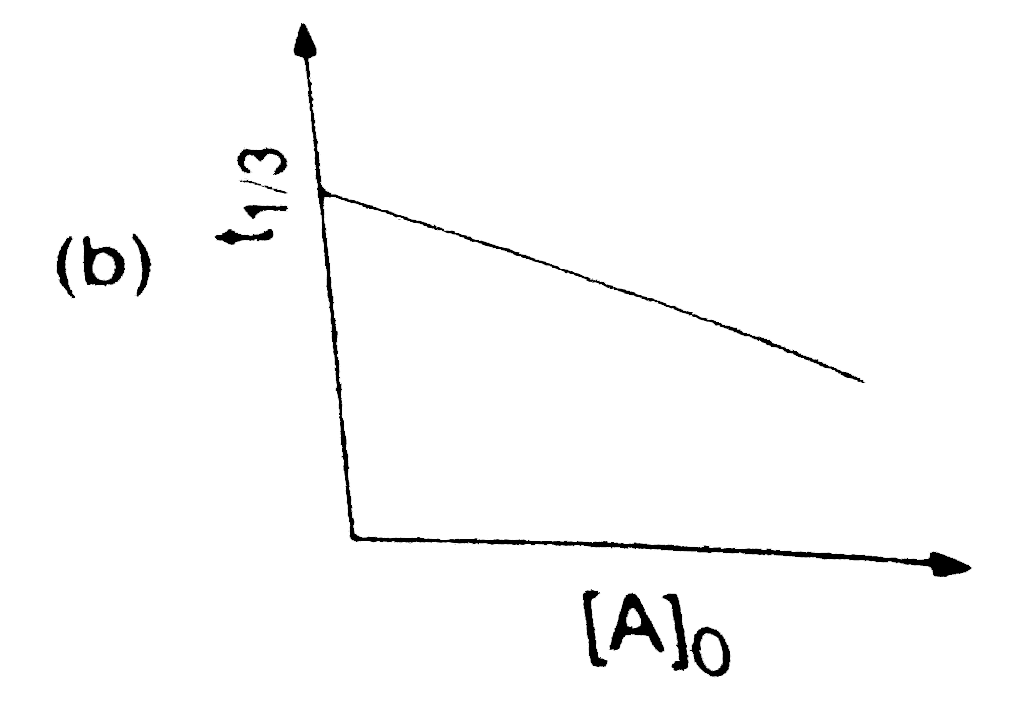
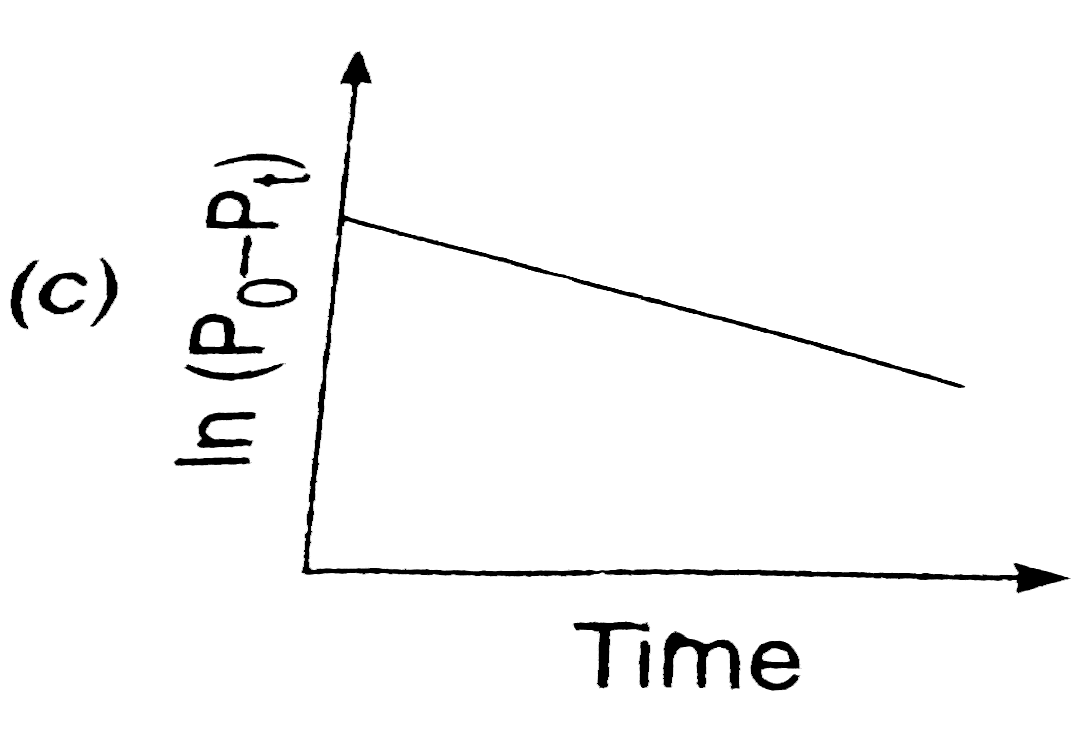
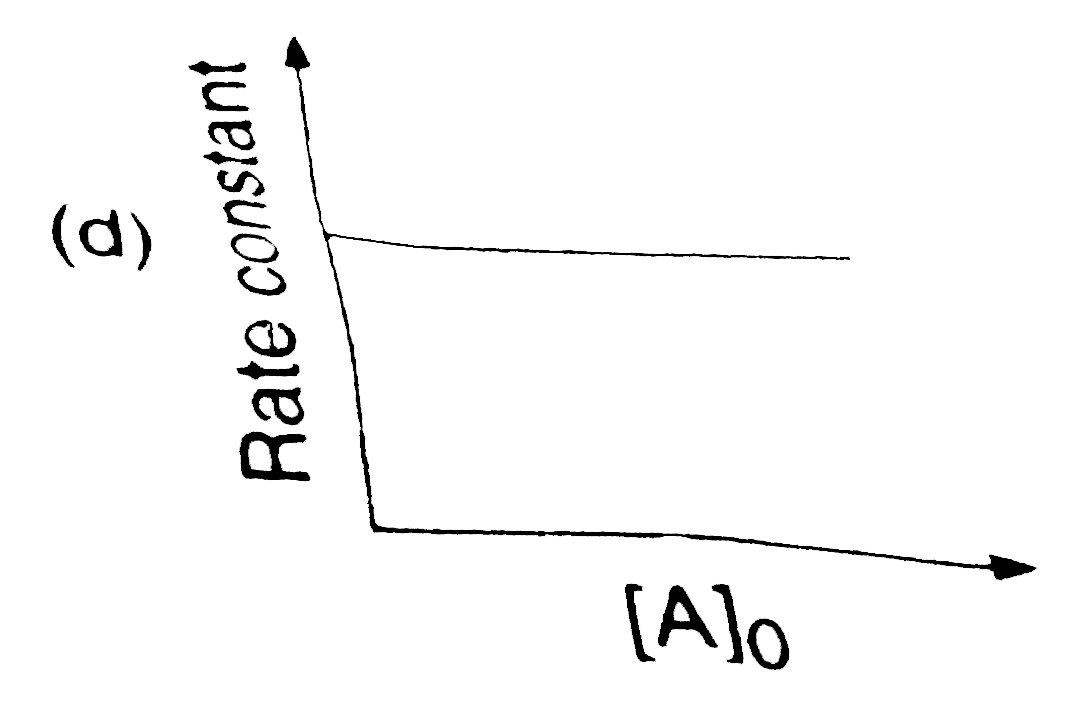
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
CHEMICAL KINETICS
OP TANDON|Exercise ASSERTION- REASON TYPE QUESTIONS|14 VideosCHEMICAL KINETICS
OP TANDON|Exercise MATRIX MATCHING TYPE QUESTIONS|11 VideosCHEMICAL KINETICS
OP TANDON|Exercise OBJECTIVE QUESTIONS (LEVEL-B) SET I|48 VideosCARBOXYLIC ACIDS AND THEIR DERIVATIVES
OP TANDON|Exercise Integer|4 VideosChemical Thermodynamics and Thermochemistry
OP TANDON|Exercise Self Assessment (Integer type).|3 Videos
Similar Questions
Explore conceptually related problems
OP TANDON-CHEMICAL KINETICS-OBJECTIVE QUESTIONS (LEVEL-B) SET II
- In the Arrhenius eqution k=Ae^(-E(a)//RT) , the rate constant (k) beco...
Text Solution
|
- Select the correct realation among the following :
Text Solution
|
- Which of the following statement are correct about the reaction in pr...
Text Solution
|
- In the Arrhenius equation , k=Ae^(-E(a)//RT) the Arrhenius constant A...
Text Solution
|
- Which of the following arepseudo uimolecular reaction?
Text Solution
|
- Rate law expression of a reaction is : Rate = k[A]^(2//3)[B] Whic...
Text Solution
|
- Which of the following are correct exression for Arrhenius equation?
Text Solution
|
- Which of the following values of the molecularity are not possible ?
Text Solution
|
- Which of the following are true for the first order reaction?
Text Solution
|
- Activation energy of forward and backward process of reaction are 60 ...
Text Solution
|
- Accroding to the Arrhenius equation
Text Solution
|
- In a bimolecular reaction, the steric factor P was experimentally dete...
Text Solution
|
- For a first order reaction A(g)rarr2B(g)+C(g) at constant volume and 3...
Text Solution
|