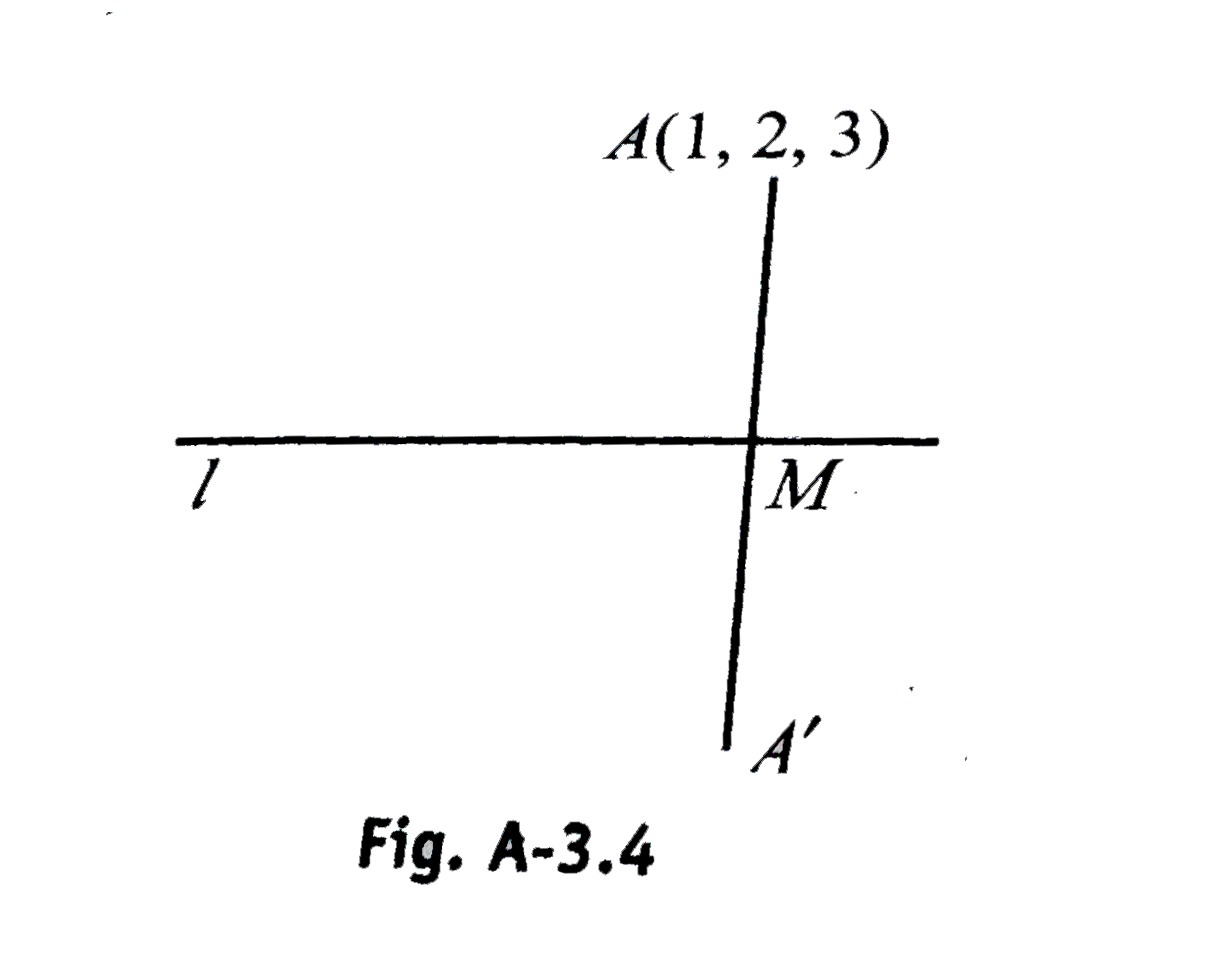Text Solution
Verified by Experts
Topper's Solved these Questions
THREE-DIMENSIONAL GEOMETRY
CENGAGE|Exercise Exercise 3.3|19 VideosTHREE-DIMENSIONAL GEOMETRY
CENGAGE|Exercise Exercise 3.4|5 VideosTHREE-DIMENSIONAL GEOMETRY
CENGAGE|Exercise Exercise 3.1|12 VideosTHREE DIMENSIONAL GEOMETRY
CENGAGE|Exercise Question Bank|20 VideosTRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONS
CENGAGE|Exercise Question Bank|34 Videos
Similar Questions
Explore conceptually related problems
CENGAGE-THREE-DIMENSIONAL GEOMETRY -Exercise 3.2
- Find the point where line which passes through point (1, 2, 3) and is ...
Text Solution
|
- Find the equation of the line passing through the points (1, 2, 3) and...
Text Solution
|
- Find the vector equation of the line passing through the point (2,-...
Text Solution
|
- Find the equation of the line passing through the point (-1,2,3) an...
Text Solution
|
- Find the equation of the line passing through the intersection (-1,...
Text Solution
|
- The straight line (x-3)/3=(y-2)/1=(z-1)/0 is Parallel to x-axis Parall...
Text Solution
|
- Find the angel between the lines 2x=3y=-za n d6x=-y=-4zdot
Text Solution
|
- If the lines (x-1)/(-3)=(y-2)/(2k)=(z-3)/(-2)a n d(x-1)/(3k)=(y-5)/1=(...
Text Solution
|
- The equations of motion of a rocket are x=2t ,y=-4ta n dz=4t , wher...
Text Solution
|
- Find the length of the perpendicular drawn from the point (5, 4, -1) t...
Text Solution
|
- Find the image of point (1,2,3) in the line (x-6)/3=(y-7)/2=(z-7)/(-2)...
Text Solution
|
- Find the shortest distance between the two lines whose vector equation...
Text Solution
|
- Find the shortest distance between the z-axis and the line, x+y+2z-...
Text Solution
|
- If the lines (x-1)/2=(y+1)/3=(z-1)/4a n d(x-3)/1=(y-k)/2=z/1 intersect...
Text Solution
|
- Let l(1) and l(2) be the two skew lines. If P, Q are two distinct poin...
Text Solution
|