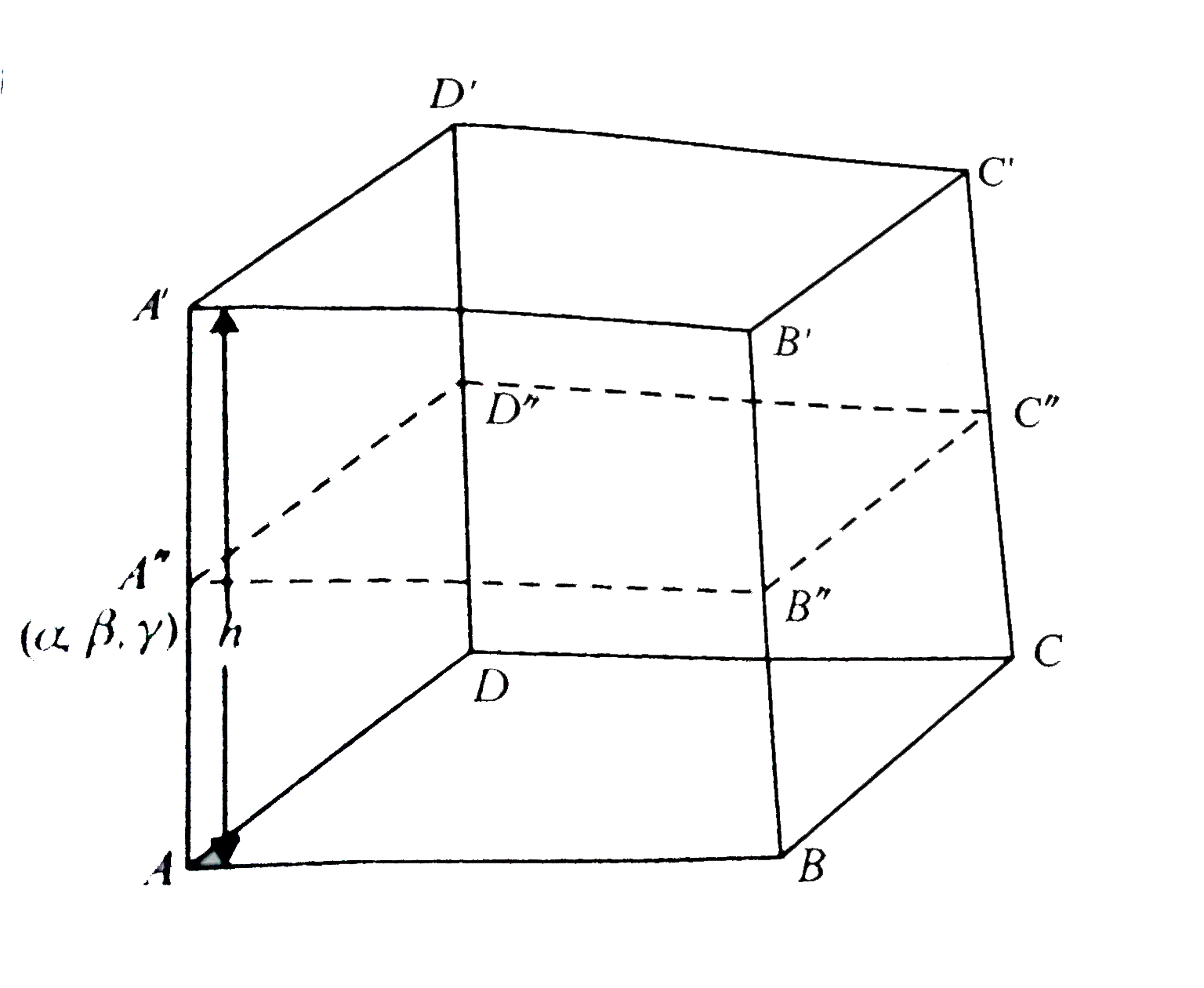Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-THREE-DIMENSIONAL GEOMETRY -JEE Previous Year
- (i) Find the equation of the plane passing through the points(2,1,0...
Text Solution
|
- Find the equation of a plane passing through (1, 1, 1) and parallel to...
Text Solution
|
- A parallelepiped S has base points A ,B ,Ca n dD and upper face points...
Text Solution
|
- Find the equation of the plane containing the lines 2x-y+z-3=0,3x+y+z=...
Text Solution
|
- A line with positive direction cosines passes through the point P(2, –...
Text Solution
|
- The value of k such that (x-4)/1=(y-2)/1=(z-k)/2 lies in the plane 2x-...
Text Solution
|
- If the lines (x-1)/2=(y+1)/3=(z-1)/4 and (x-3)/1=(y-k)/2=z/1 intersect...
Text Solution
|
- A variable plane at distance of 1 unit from the origin cuts the coordi...
Text Solution
|
- A plane passes through (1,-2,1) and is perpendicualr to two planes 2x...
Text Solution
|
- Let P(3,2,6) be a point in space and Q be a point on line vec r=( hat...
Text Solution
|
- Equation of the plane containing the straight line x/2=y/3=z/4 and per...
Text Solution
|
- If the distance of the point P(1,-2,1) from the plane x+2y-2z=alpha...
Text Solution
|
- The point P is the intersection of the straight line joining the point...
Text Solution
|
- Perpendiculars are drawn from points on the line (x+2)/2=(y+1)/(-1)=z...
Text Solution
|
- Two lines L1x=5, y/(3-alpha)=z/(-2)a n dL2: x=alphay/(-1)=z/(2-alpha) ...
Text Solution
|
- A line l passing through the origin is perpendicular to the lines l1: ...
Text Solution
|
- let L be a straight line passing through the origin. Suppose that all ...
Text Solution
|
- In R^(3), consider the planes P(1):y=0 and P(2),x+z=1. Let P(3) be a p...
Text Solution
|
- Consider the planes 3x-6y-2z=15a n d2x+y-2z=5. Statement 1:The parame...
Text Solution
|
- Consider three planes P(1):x-y+z=1 P(2):x+y-z=-1 and " "P...
Text Solution
|