Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN-TRIGNOMETRIC FUNCTIONS-MISCELLANEOUS EXERCISE
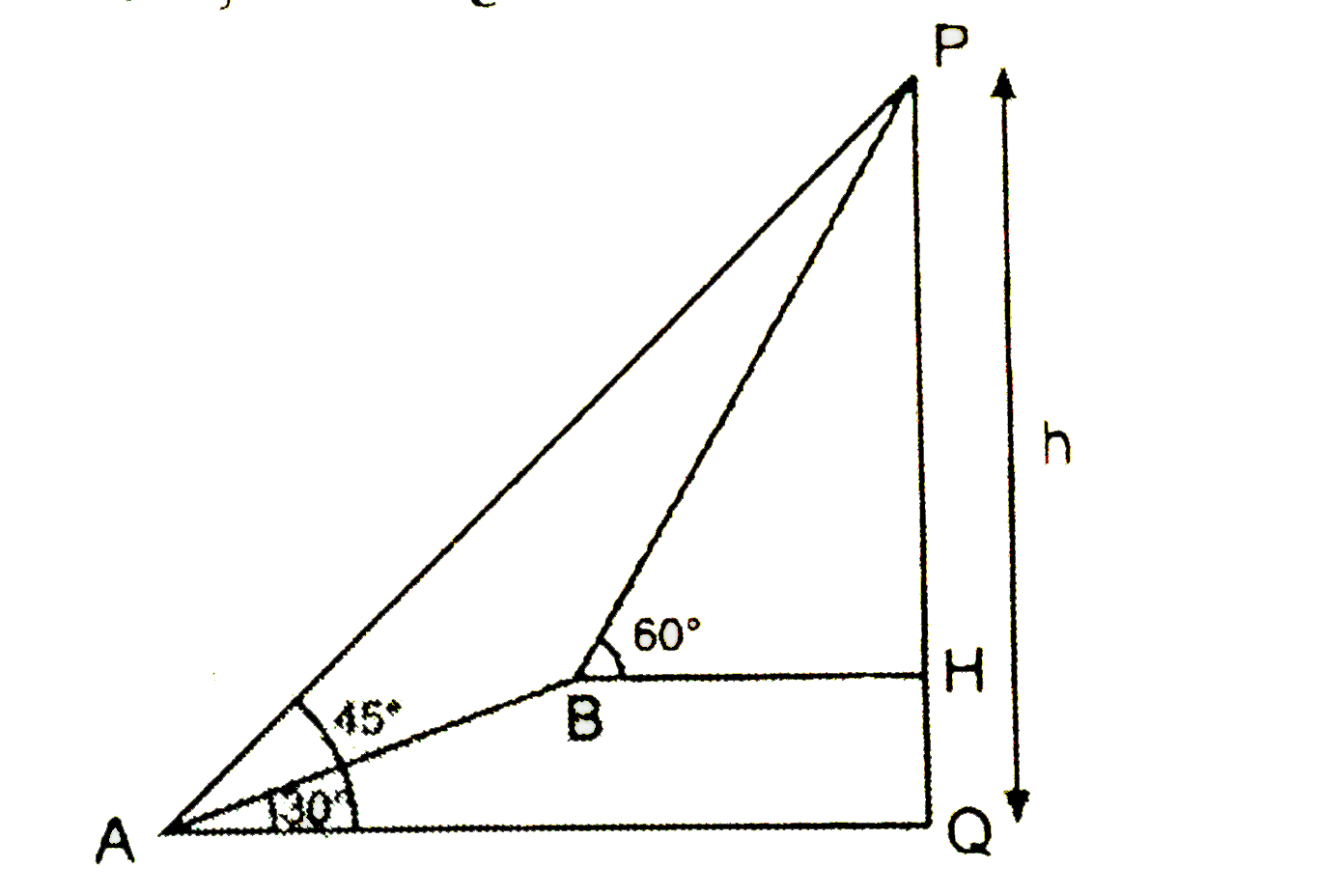
- The angle of elevation of the highest point P of a vertical tower at p...
Text Solution
|
- 2cos(pi/13)cos(9pi/13)+cos(3pi/13)+cos(5pi/13)=0
Text Solution
|
- (sin 3x + sin x) sin x + (cos 3x - cos x) cos x =0
Text Solution
|
- (cosx+cosy)^(2)|(sinx-siny)^(2)=4cos^(2)(x+y)/(2)
Text Solution
|
- (cosx-cosy)^(2)+(sinx-siny)^(2)=?
Text Solution
|
- Prove that: s in" "x" "+" "s in" "3x" "+" "s in" "5x" "+" "s in" "7x" ...
Text Solution
|
- Prove that: ((sin7x+sin5x)+(sin9x+sin3x))/((cos7x+cos5x)+(cos9x+cos3x)...
Text Solution
|
- sin3x+sin2x-sinx=4sinxcos(x/2)cos(3x/2)
Text Solution
|
- Find sinx/2,cosx/2and tanx/2of the following : tanx=-4/3,xin quadrant ...
Text Solution
|
- cosx=-1/3, x in quadrant III. Find the values of other five trignometr...
Text Solution
|
- sinx=1/4, x in quadrant II. Find the values of other five trignometric...
Text Solution
|