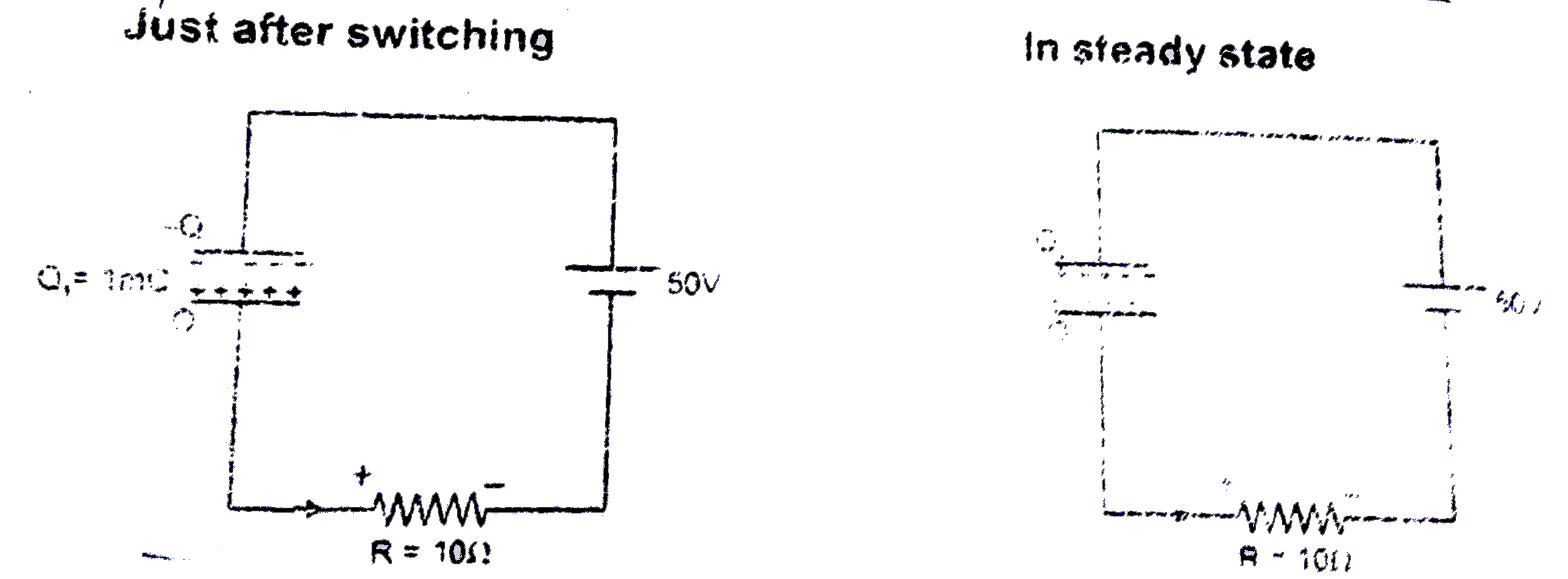A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
RESONANCE-ALTERNATING CURRENT-Exercise -3 Part-1
- An AC voltage source of variable angular frequency (omega) and fixed a...
Text Solution
|
- A sereis R-C circuit is connected to AC voltage source. Consider two c...
Text Solution
|
- A series R-C combination is connected to an AC voltage of angular freq...
Text Solution
|
- In the given circuit, the AC source has (omega) = 100 rad//s. Consider...
Text Solution
|
- A thermal power plant produed electric power of 600kW at 4000V, which ...
Text Solution
|
- A thermal power plant produed electric power of 600kW at 4000V, which ...
Text Solution
|
- At time t = 0, terminal A in the circuit shown in the figure is connec...
Text Solution
|
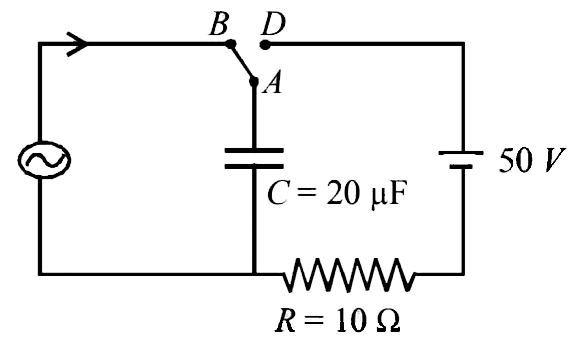 .
.