Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
RESONANCE-WAVE OPTICS-Advanced Level Problems
- In YDSE with D = 1 m, d = 1 mm, light of wavelength 500 nm is incident...
Text Solution
|
- Two parallel beams of light P and Q (separation d) containing radiatio...
Text Solution
|
- White coherent light (400 nm-700 nm) is sent through the slits of a Yo...
Text Solution
|
- A beam of light consisting of two wavelenths, 6500 Å and 5200 Å is use...
Text Solution
|
- A source S is kept directly behind the slit S(1) in a double slit appa...
Text Solution
|
- A monochromatic light of lambda=500 nm is incident on two identical sl...
Text Solution
|
- In a YDSE experiment, the distance between the slits & the screen is 1...
Text Solution
|
- In a YDSE a parallel beam of light of wavelength 6000Å is incident on ...
Text Solution
|
- An equil convex lens of focal length 10 cm (in air) and R.l.4//3 is pu...
Text Solution
|
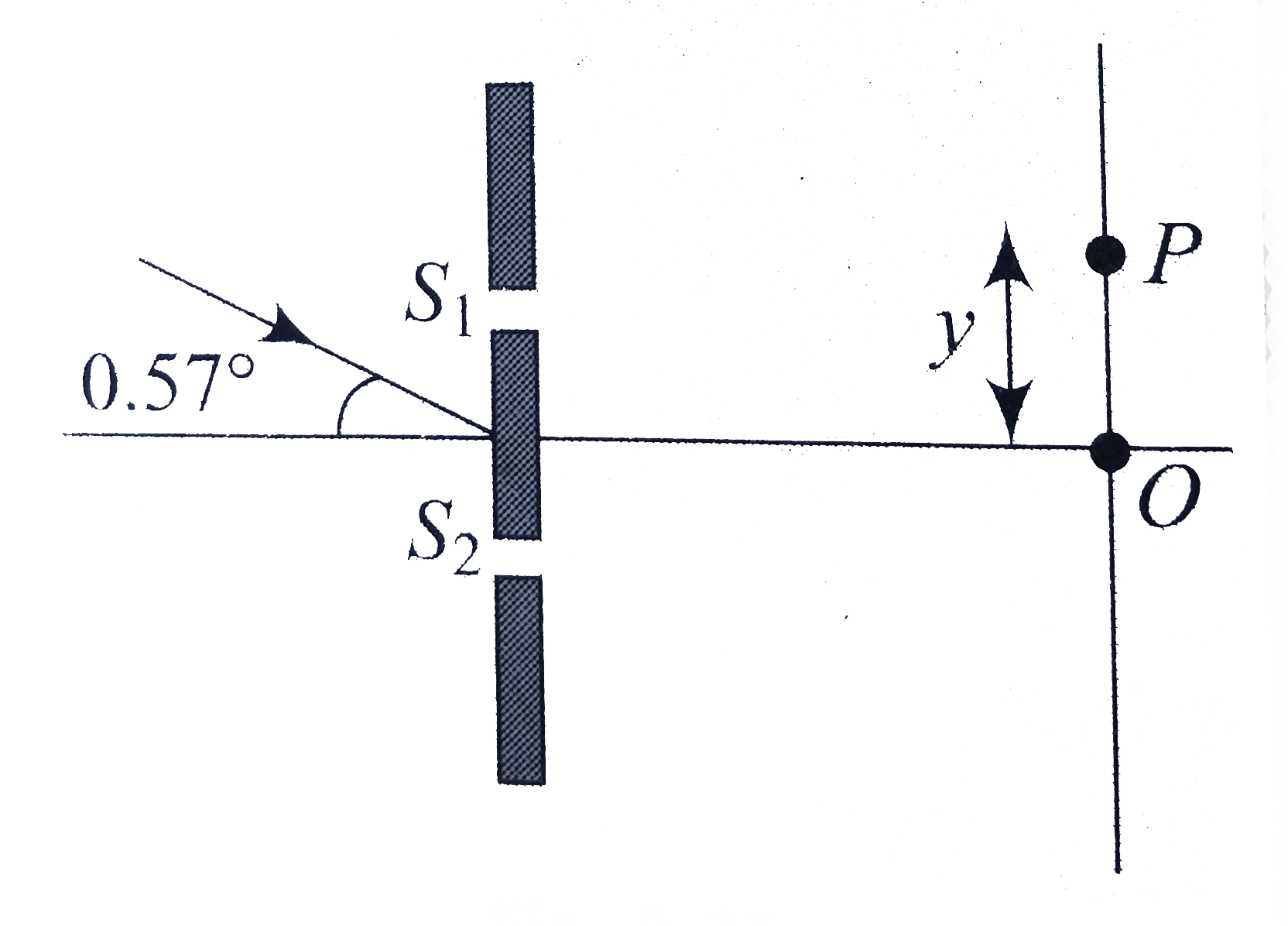 .
.