Similar Questions
Explore conceptually related problems
Recommended Questions
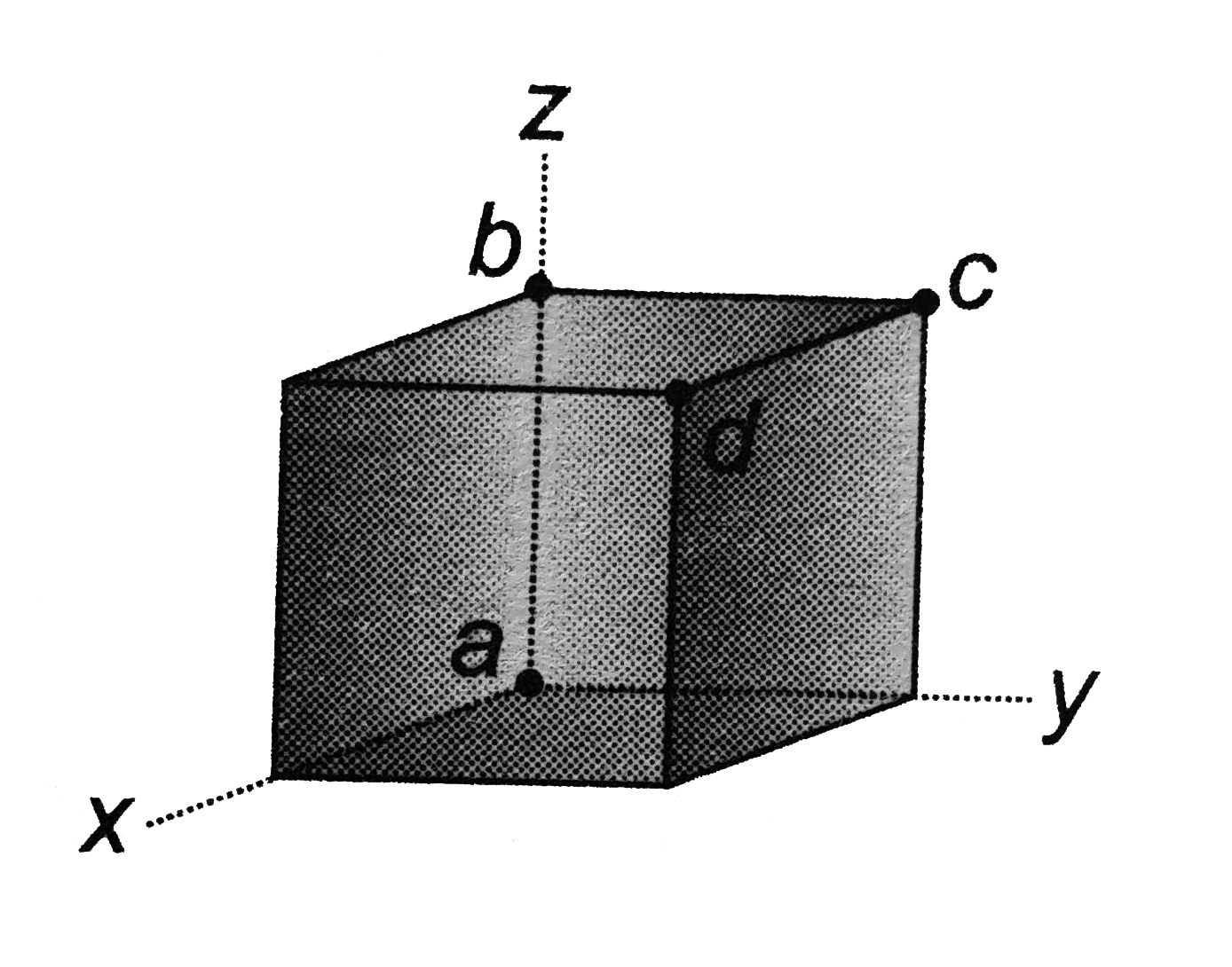
- A cube is placed so that one corner is at the origin and three edges a...
Text Solution
|
- A cube is placed so that one corner is at the origin and three edges a...
Text Solution
|
- Find the angle between the diagonals of a cube with edges of length "a...
Text Solution
|
- एक रेखा X,Y तथा Z अक्षो के साथ क्रमश 90^(@),135^(@),45^(@) का कोण बना...
Text Solution
|
- The direction rations of the diagonals of a cube which joins the origi...
Text Solution
|
- If three vectors along coordinate axis represent the adjacent sides of...
Text Solution
|
- यदि कोई रेखा x^(-) और y-अक्षों के साथ क्रमशः 30^(@) और 60^(@) का को...
Text Solution
|
- दिये गये चित्र में घन की प्रत्येक भुजा में 1 ओम का प्रतिरोध जोड़ा गया ह...
Text Solution
|
- एक रेखा x- अक्ष तथा y-अक्ष से क्रमशः 120^@ तथा 60^@ के कोण बनाती है , ...
Text Solution
|