Home
Class 11
CHEMISTRY
Variation of equiibrium constant K with ...

Variation of equiibrium constant `K` with temperature `T` is given by van `'t` Holf equation,
`log K=logA-(DeltaH^(@))/(2.303RT)`
A graph between log `K` and `T^(-1)` was a straight line as shown in the figure and having `theta=tan^(-1)(0.5)"and"OP=10`. Calculate:
(a) `DeltaH^(@)` (standard heat of reaction)when `T=300K,`
(b) `A` (pre-exponetial factor),
(c) Equilibrium constant `K` at `300 K,`
(d) `K "at" 900 K "if" DeltaH^(@)` is independent of temperature.

Text Solution

Verified by Experts

The correct Answer is:
(a) `9.574J mol^(-1);` (b)`A=10^(10);` (c) `9.96xx10^(9);` (d)`9.98xx10^(9)`
(a) `log_(10)K=log_(10)A-(DeltaH_(@))/(2.303RT)`
It is an equation of a straight line of the type `y=c+mx`
Slope 'm'=`tan0=(DeltaH^(@))/(2.303R)`
`0.5=(DeltaH^(@))/2.303xx8.314`
`DeltaH^(@)=9.574J mol^(-1)`
(b) `"Intercept",C'=log_(10)A=10` `A=10^(10)`
(c) `log K=10-(9.574)/(2.303xx8.314xx298)`
`K=9.96xx10^(9)`
(d) `log((K_(2))/(K_(1)))=(DeltaH)/2.303R {(1)/(T_(1))-(1)/(T_(2))}`
`log (K_(2))/(9.96xx10_(9))=(9.574)/(2.303xx8.314) {(1)/(298)-(1)/(798)}`
On solving `K_(2)=9.98xx10_(9)`
Promotional Banner

Topper's Solved these Questions

  • CHEMICAL EQUILIBRIUM

    RESONANCE|Exercise (MSPs)|8 Videos

  • CHEMICAL EQUILIBRIUM

    RESONANCE|Exercise Board Level Exercise|33 Videos

  • CHEMICAL EQUILIBRIUM

    RESONANCE|Exercise Advanced Level Problems (Part-3)(Stage-5)|2 Videos

  • CHEMICAL BONDING

    RESONANCE|Exercise Inorganic chemistry (Chemistry Bonding)|49 Videos

  • D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS

    RESONANCE|Exercise Match the column|1 Videos

Similar Questions

Explore conceptually related problems

The graph between log k versus 1//T is a straight line.

For a hypothetical reaction: A(g) +B(g) hArr C(g) +D(g) a graph between log K_(eq) and T^(-) is striaght line as follows, where theta = tan^(-1) 0.5 and OA = 1.0 (S.I. units) Assuming DeltaH^(@) is independent of temperature, the equilibrium constant at 298 K will be:

A graph plotted between log_(10) K_(c) and 1//T is straight line with intercept 10 and slpoe equal t0 0.5. Calculate : ( i ) pre -exponential factor A . ( ii ) heat of reaction at 298 K . ( iii ) equilibrium constant at 298 K . ( iv ) equilibrium constant in at 800 k assuming DeltaH remains constant in between 298 K and 800 K .

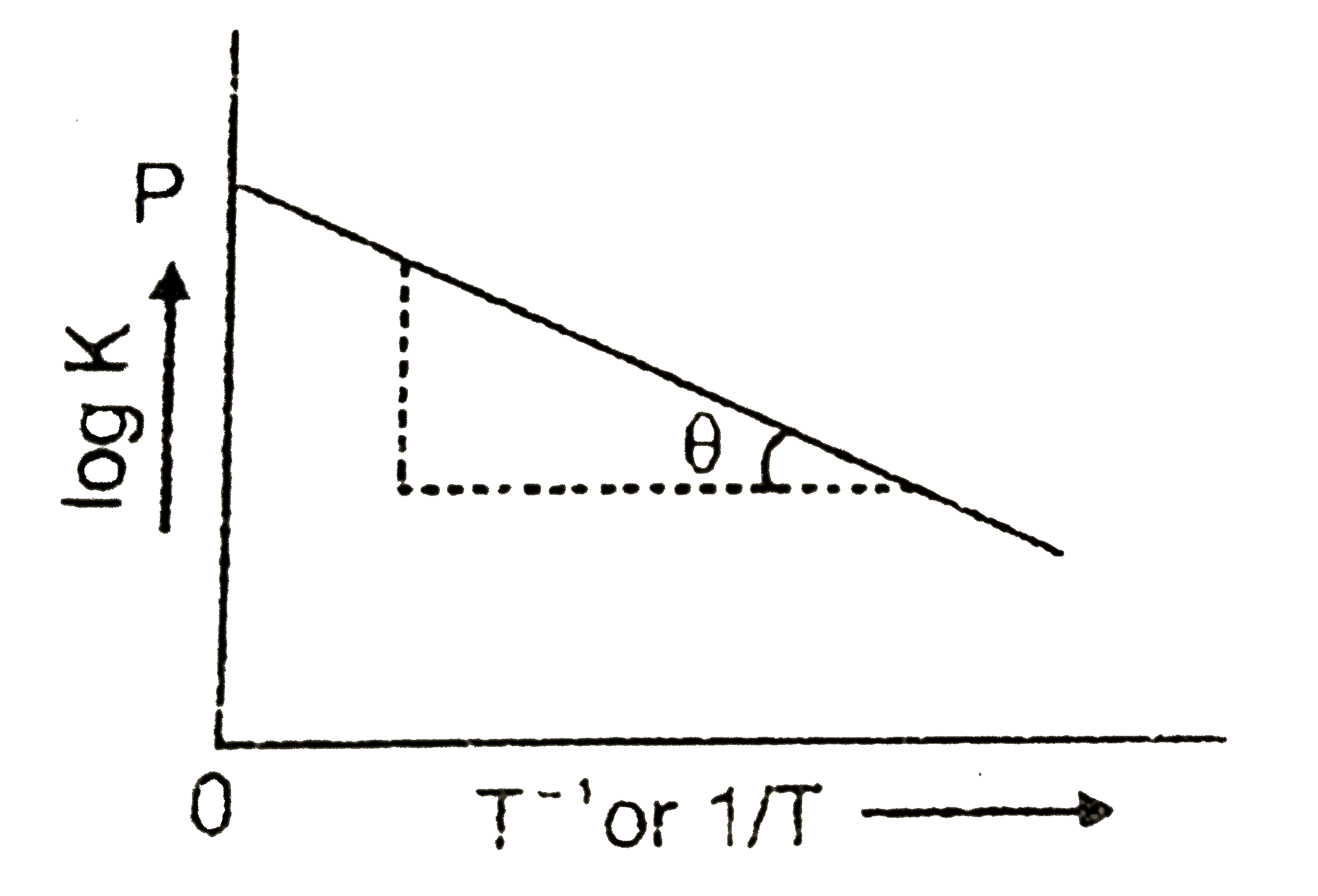
Variation of equilibrium constan K with temperature is given by van't Hoff equation InK=(Delta_(r)S^(@))/R-(Delta_(r)H^(@))/(RT) for this equation, (Delta_(r)H^(@)) can be evaluated if equilibrium constans K_(1) and K_(2) at two temperature T_(1) and T_(2) are known. log(K_(2)/K_(1))=(Delta_(r)H^(@))/(2.303R)[1/T_(1)-1/T_(2)] Select the correct statement :

The variation of rate constant with temperature is given by the integrated from of the Arrhenius equation, log_10k = (-Ea)/(2.303 RT) + constant where k = rate cosntant and Ea is the experimental activation energy. If for a certain reaction, log_10k = (-3163.0)/T + 11.899 , calculate Ea.

Rate constant k varies with temperature by equation, log k (min+^(-1))=5-(2000)/(T(K)) We can conclud:

Graph between log k and 1//T [ k rate constant (s^(-1)) and T and the temperature (K) ] is a straight line with OX =5, theta = tan^(-1) (1//2.303) . Hence -E_(a) will be