Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-HIGHT AND DISTANCE -JEE Previous Year
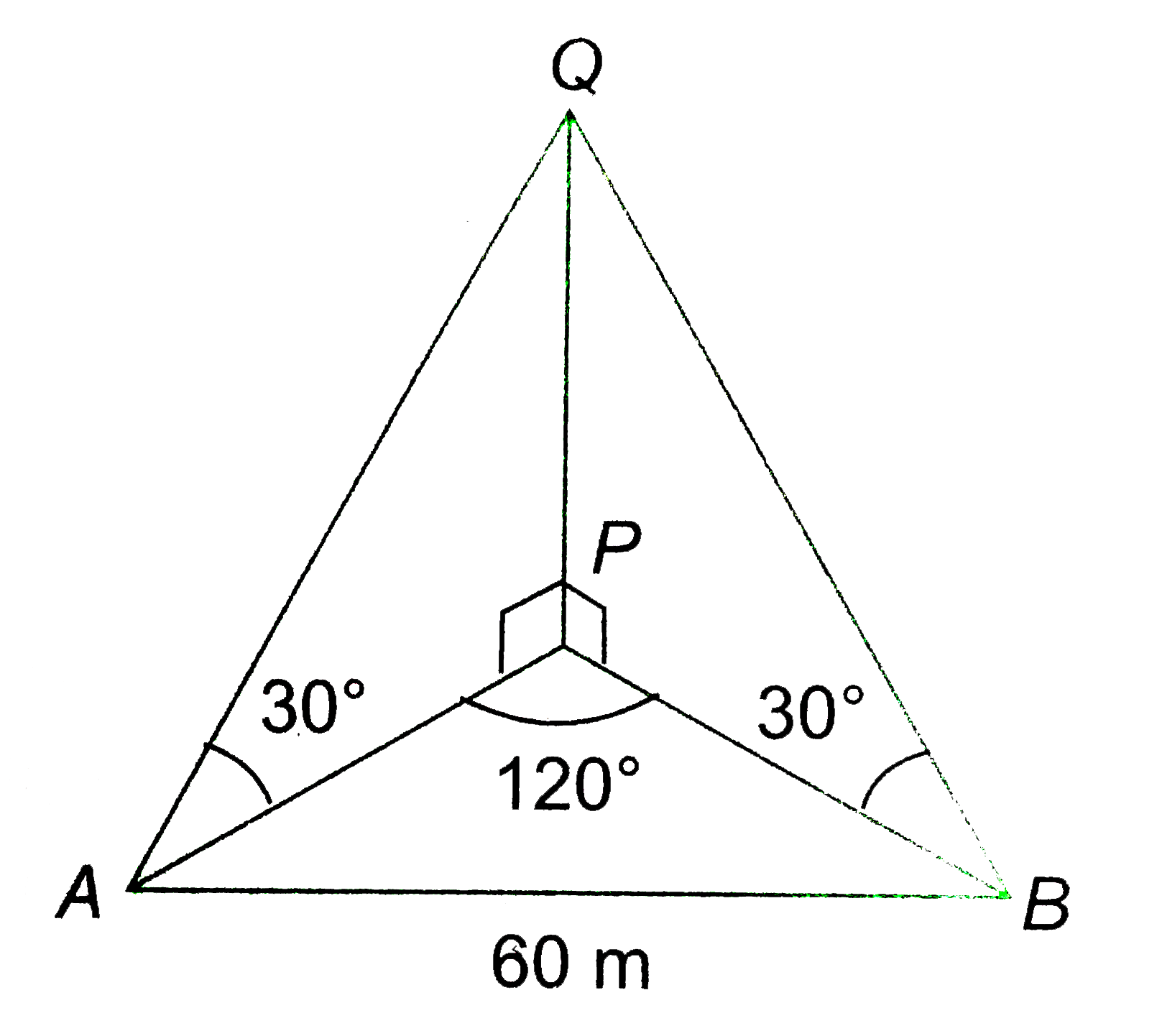
- A vertical tower PQ subtends the same anlgle of 30^@ at each of two po...
Text Solution
|
- A bird is sitting on the top of a vertical pole 20 m high and its e...
Text Solution
|
- If the angles of elevation of the top of a tower from three colline...
Text Solution
|
- PQR is a triangular park with PQ=PR=200m . A T.V tower stands at the m...
Text Solution
|