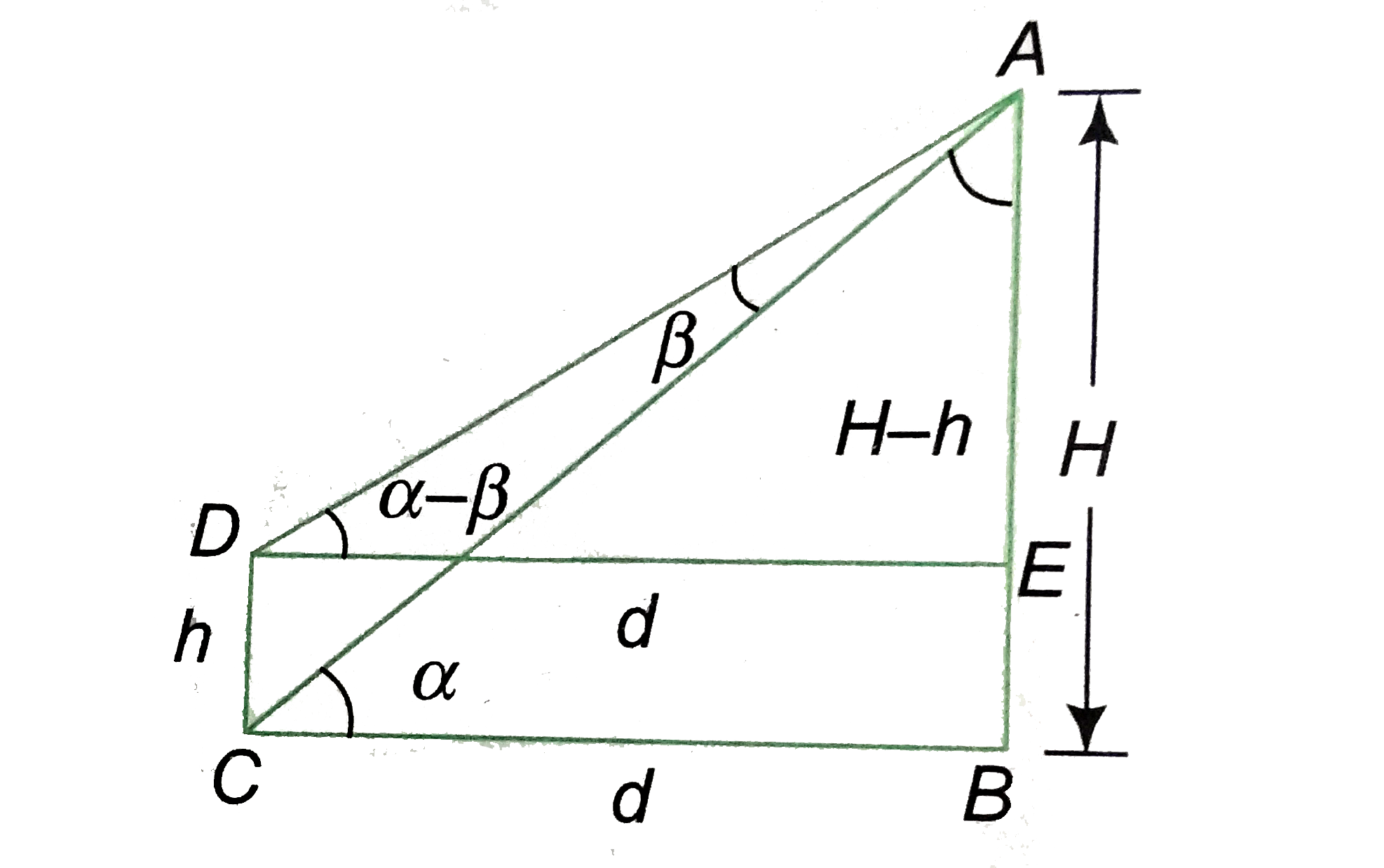
From the bottom of a pole of height h, t...

From the bottom of a pole of height h, the angle of elevation of the top of a tower is `alpha`. The pole subtends an angle `beta` at the top of the tower. find the height of the tower.

`(hcot (alpha - beta ))/(cot (alpha - beta )- cot alpha`

`(h tan (alpha- beta))/(tan(alpha- beta ) - tan alpha)`

`(cot (alpha- beta))/(cot (alpha - beta)-cot alpha)`

None of these

Text Solution

Verified by Experts

Let AB be the tower of height H and CD be the pole

In triangle ABC, d =`hcotalpha`
In triangle AED,d `=(H-h)cot (alpha - beta)`
`rArr Hcotalpha= (H-h) cot(alpha-beta)`
`therefore H=(h cot (alpha - beta))/(cot (alpha - beta )- cot alpha `

Topper's Solved these Questions

HIGHT AND DISTANCE
CENGAGE|Exercise JEE Previous Year|3 Videos
HIGHT AND DISTANCE
CENGAGE|Exercise JEE Previous Year|3 Videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
CENGAGE|Exercise Exercise|22 Videos
HYPERBOLA
CENGAGE|Exercise JEE Advanced Previous Year|14 Videos

Similar Questions

Explore conceptually related problems

From the bottom of a pole of height h, the angle of elevation of the top of the tower is alpha . The pole subtends an angle beta at the top of the tower. Prove that the height of the tower is h sin alpha " cosec "beta cos(alpha - beta)

The angle of elevation of the top of a tower at a point on the ground, 50 m away from the foot of the tower, is 60°. Find the height of the tower.

The angle of elevation of the top of a tower from a point on the ground,which is 30m away from the foot of the tower is 30o. Find the height of the tower.

From the top of a cliff 15mt height, the angle of elevation of the top of a tower is found to be equal to the angle of depression of the foot of the tower.The height of the tower is

From the top of a 7m high building,the angle of elevation of the top of a tower is 60 and the angle of depression of the foot of the tower is 30. Find the height of the tower.

The angle of elevation of the top of a tower from a point on the ground,which is 30m away from the foot of the tower,is 30^(@). Find the height of the tower.

CENGAGE-HIGHT AND DISTANCE -Exercise

The tops of two poles of height 20 m and 14 m are connected by a wi...
Text Solution
|
The angle of elevation of the top of an unfinished tower at a distanc...
Text Solution
|
A tower of height b subtends an angle at a point 0 on the ground level...
Text Solution
|
A ladder rest against a wall making an angle alpha with the horizontal...
Text Solution
|
Two hagstaffs stand on a horizontal plane. A and B are two points on t...
Text Solution
|
A snake observes an eagle perching on the top of a pole 20 m high. Its...
Text Solution
|
For a man , the angle of elevation of the highest point of a tower sit...
Text Solution
|
A flagstaff stands in the centre of a rectangular field whose diagona...
Text Solution
|
AB is a vertical pole resting at the end A on the level ground. P is ...
Text Solution
|
From the bottom of a pole of height h, the angle of elevation of the t...
Text Solution
|
A tower of height b subtends an angle alpha at a point on the same lev...
Text Solution
|
A man standing on a level plane observes the elevation of the top of a...
Text Solution
|
5 m high pole stands on a building of height 25 m. The pole and the bu...
Text Solution
|
A vertical tower stands on a declivity which isinclined at 15^@ to the...
Text Solution
|
The length of the shadow of a pole inclined at 10^@ to the vertical t...
Text Solution
|
A tower subtends angles alpha,2alpha,3alpha respectively, at point A ,...
Text Solution
|
A harbour lies in a direction 60^@ south - west from a fort and at a d...
Text Solution
|
A tower AB leans towards west making an angle alpha with the vertical...
Text Solution
|