Text Solution
Verified by Experts
NCERT-AREAS RELATED TO CIRCLES-EXERCISE 12.1
- Tick the correct answer in the following and justify your choice : If...
Text Solution
|
- The wheels of a car are of diameter 80 cm each. How many complete rev...
Text Solution
|
- The radii of two circles are 19 cm and 9 cm respectively. Find the ra...
Text Solution
|
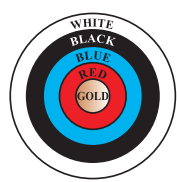
- Fig. 12.3 depicts an archery target marked with its five scoring area...
Text Solution
|
- The radii of two circles are 8 cm and 6 cm respectively. Find the rad...
Text Solution
|