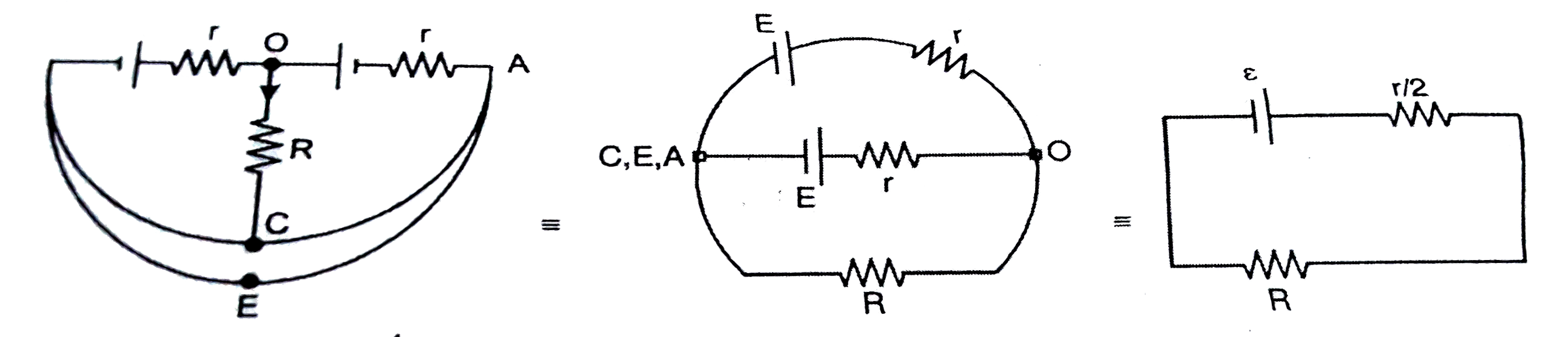
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Solve problem 15 if the length of rod is 2L and resistance 2r and it i...
Text Solution
|
- A rod of length L and resistance r rotates about one end as shown in ....
Text Solution
|
- Solve problem 15 if the length of rod is 2L and resistance 2r and it i...
Text Solution
|
- A conducting rod of length 2l is rotating with constant angular speed ...
Text Solution
|
- Solve the above question if the length of rod is 2L and resistance 2r ...
Text Solution
|
- In the figure there are two identical conducting rods each of length a...
Text Solution
|
- A long thin rod of length 2L rotates with a constant angular accelerat...
Text Solution
|
- A long thin rod of length 2L rotates with a constant angular accelerat...
Text Solution
|
- A long thin rod of length 2L rotates with a constant angular accelerat...
Text Solution
|