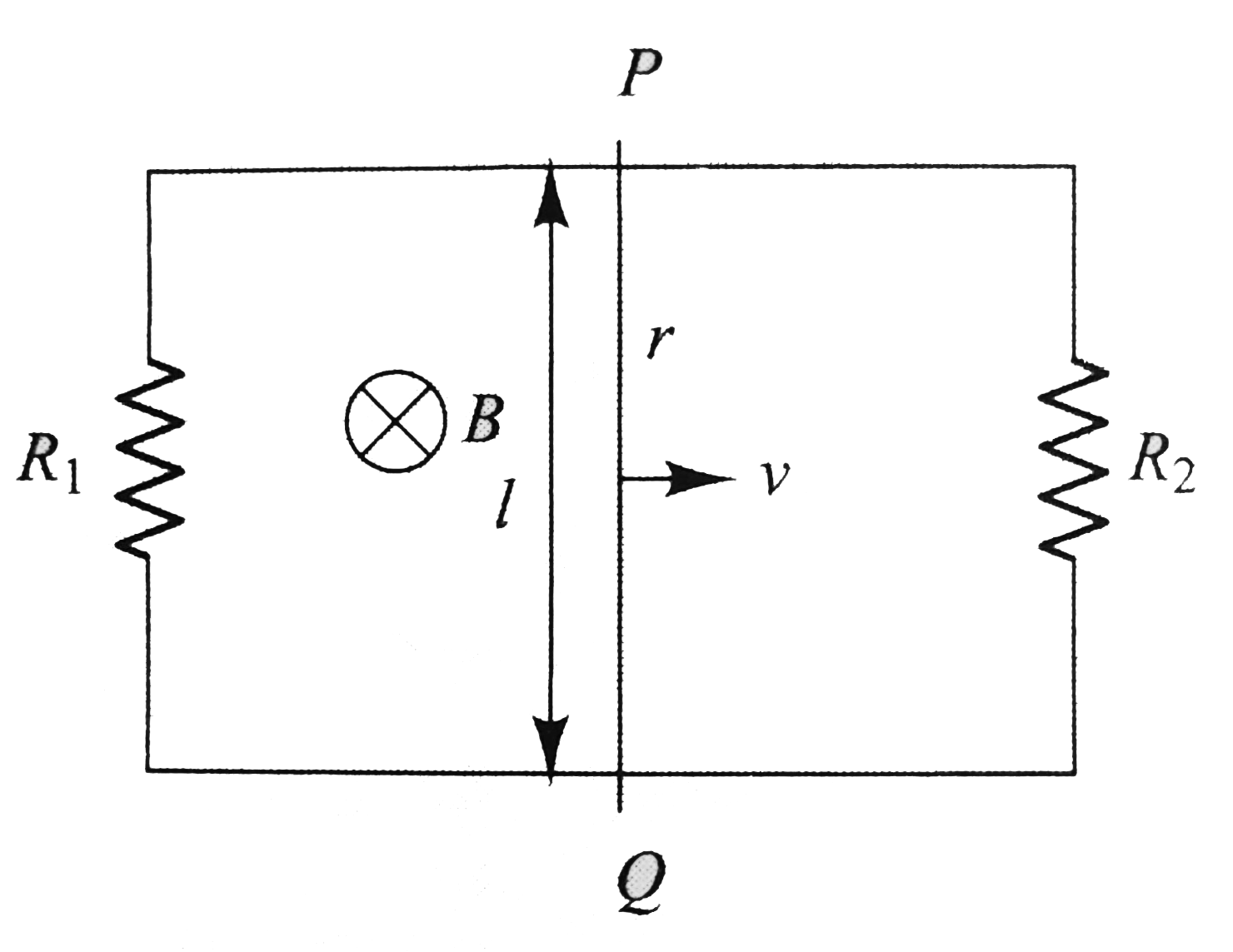
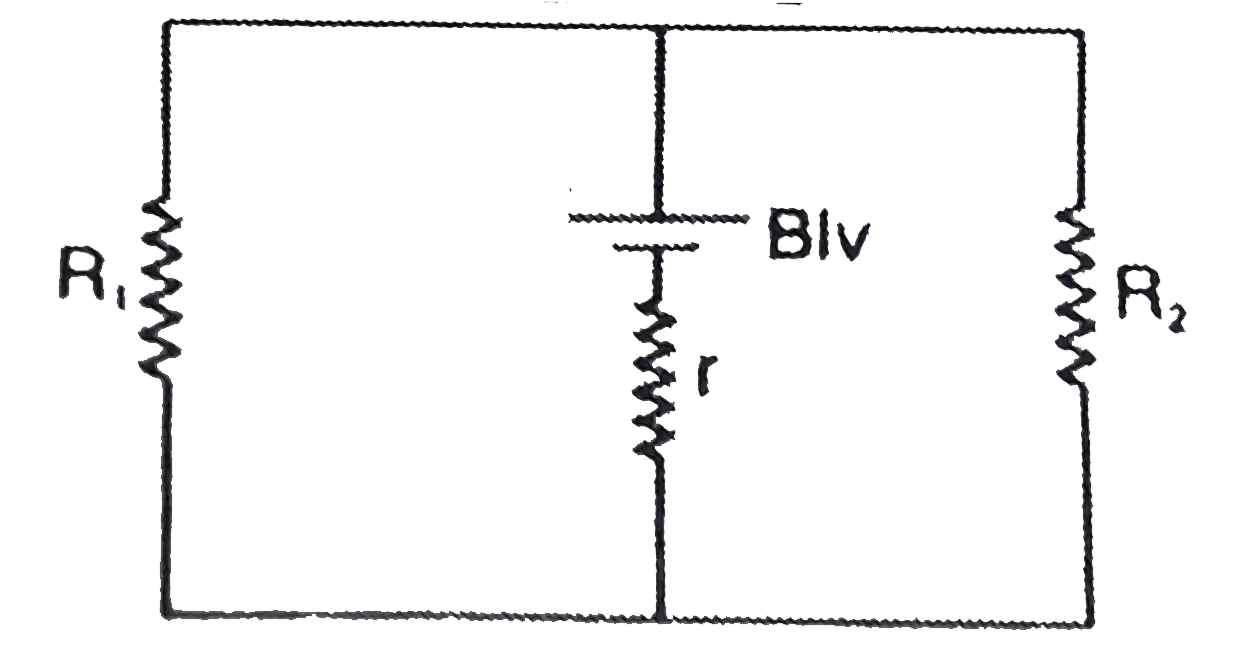
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Shows rod PQ of mass m and resistance r moving on two fixed, resistanc...
Text Solution
|
- Shows rod PQ of mass m and resistance r moving on two fixed, resistanc...
Text Solution
|
- Two long parallel conducting rails are placed in a uniform magnetic fi...
Text Solution
|
- Two long parallel conducting rails are placed in a uniform magnetic fi...
Text Solution
|
- Two long parallel conducting rails are placed in a uniform magnetic fi...
Text Solution
|
- A uniform rod of mas m is moving with constant velocity v(0) in a perp...
Text Solution
|
- Two parallel fixed conducting rails are l distance apart. They are con...
Text Solution
|
- A rod of mass m and resistance r is placed on fixed, resistanceless, s...
Text Solution
|
- A uniform metal rod is moving with a uniform velocity v parallel to a ...
Text Solution
|