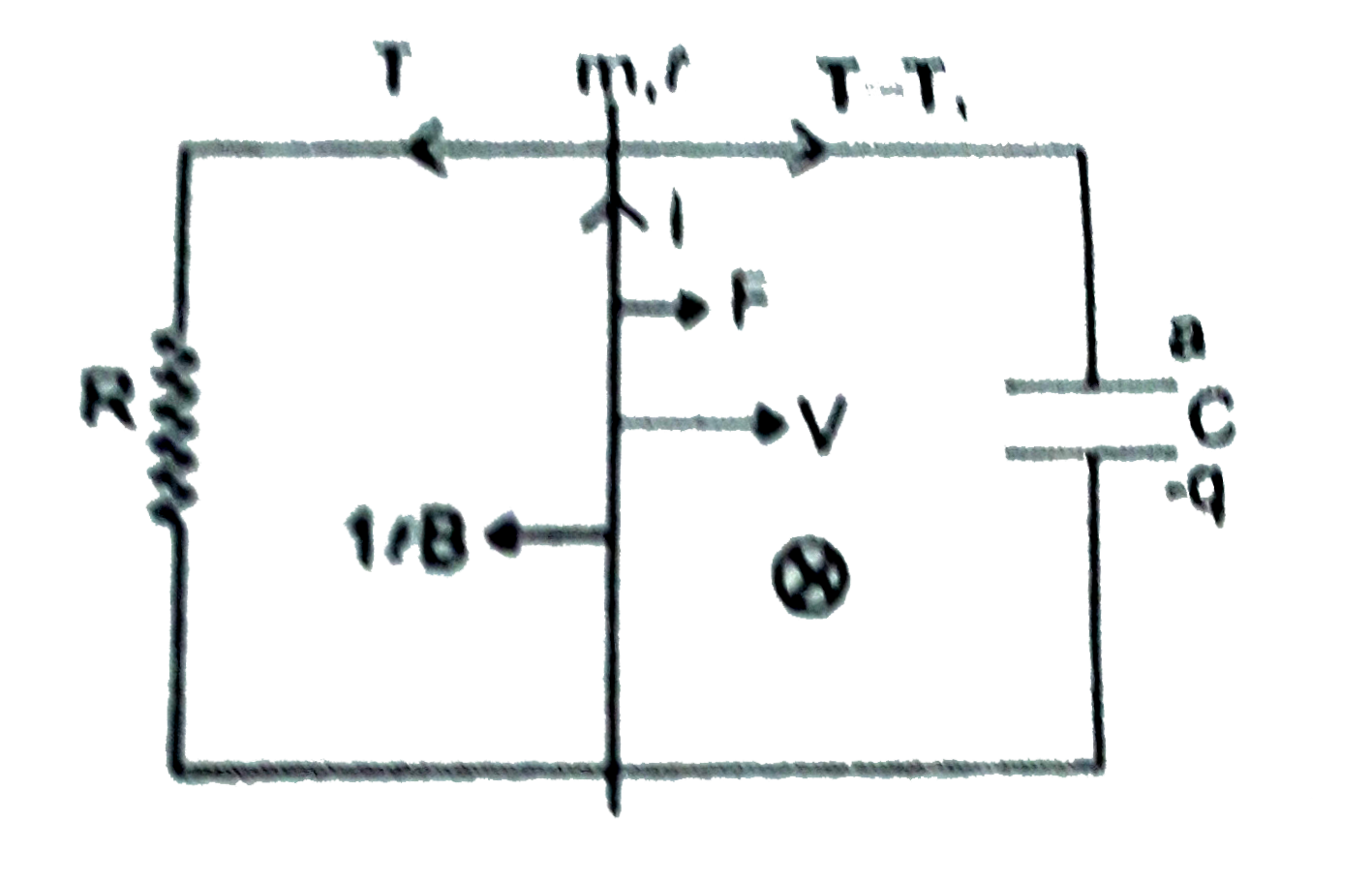
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Find the velocity of the moving rod at time t if the initial velocity ...
Text Solution
|
- Two points of a rod move with velocity 3 v and v perpendicular to the ...
Text Solution
|
- A conducting rod AB moves parallel to x-axis in the x-y plane. A unifo...
Text Solution
|
- A conducting rod of resistence r moves uniformely with a constant spee...
Text Solution
|
- in the above equation if a constant force F is applied on the rod.Find...
Text Solution
|
- Find the velocity of the moving rod at time t if the initial velocity ...
Text Solution
|
- In the above question if a constant force F is applied on the rod. Fin...
Text Solution
|
- Find the velocity of the moving rod at time t if the initial velocity ...
Text Solution
|
- In the above question if a constant force F is applied on the rod. Fin...
Text Solution
|