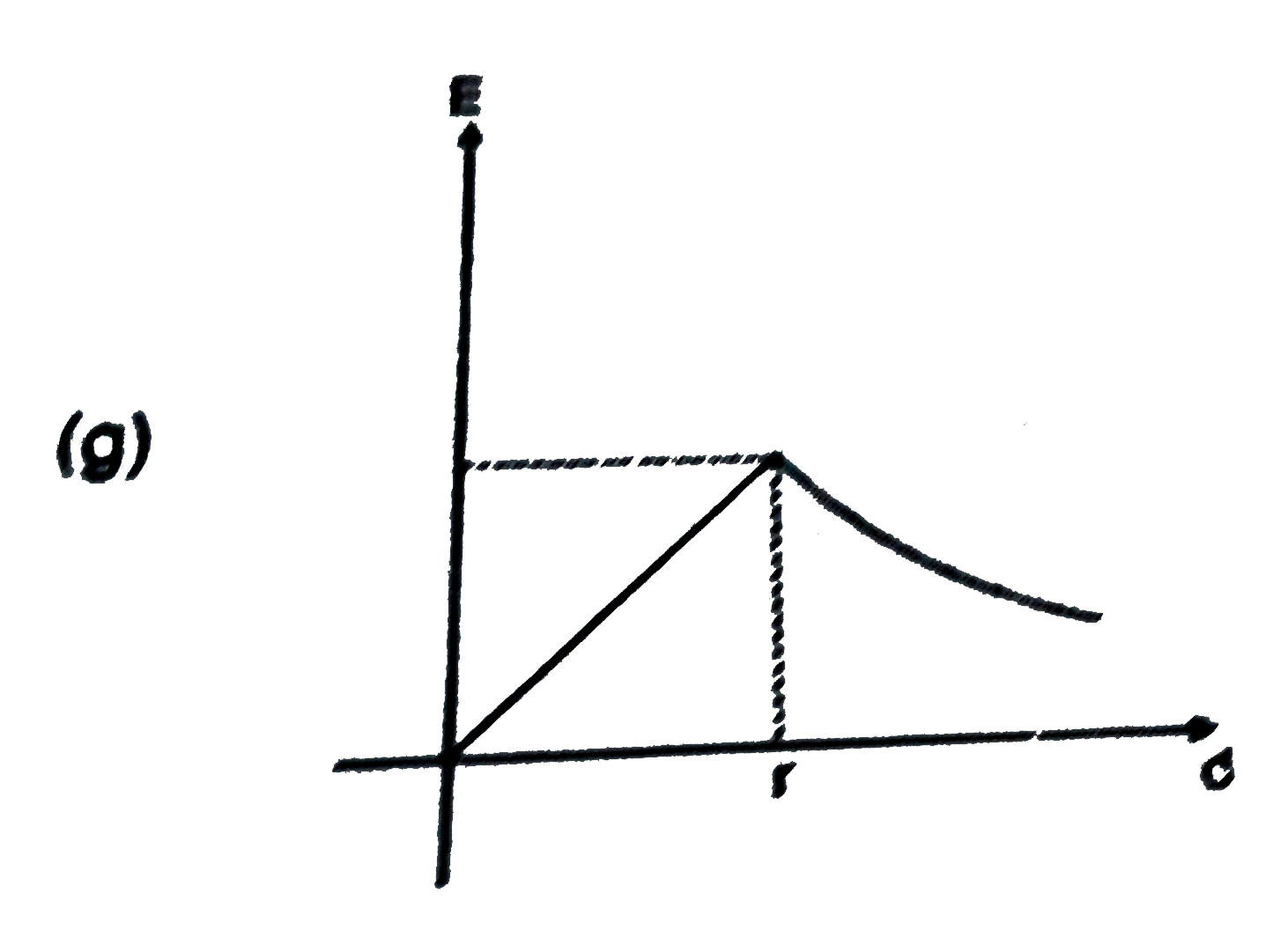
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A long solenoid of length l=2.0 m , radius r=0.1 m and total number of...
Text Solution
|
- A long solenoid has a radius a and number of turns per unit length is ...
Text Solution
|
- The expression for magnetic induction inside a solenoid of length L ca...
Text Solution
|
- A long solenoid of length l=2.0 m , radius r=0.1 m and total number of...
Text Solution
|
- A long solenoid has 800 turns per metre length of solenoid A current o...
Text Solution
|
- Obtain the expression for the magnetic energy stored in a solenoid in ...
Text Solution
|
- A long solenoid carrying a current produces a magnetic field B along i...
Text Solution
|
- A solenoid carrying 1 A current has a length of 1 m and contains 10000...
Text Solution
|
- A long solenoid of length 'l' having carries a current I. Deduce the e...
Text Solution
|