Home
Class 12
PHYSICS
In the circuit shown in fig. E(1)=3" vol...

In the circuit shown in fig. `E_(1)=3" volt",E_(2)=2" volt",E_(3)=1" vole and "R=r_(1)=r_(2)=r_(3)=1`ohm.
(i) Find potential difference in Volt between the points A and B with A & B unconnected.
(ii) If `r_(2)` is short circuited and the point A is coneted to point B through a zero resistance wire, find the current through R in ampere.

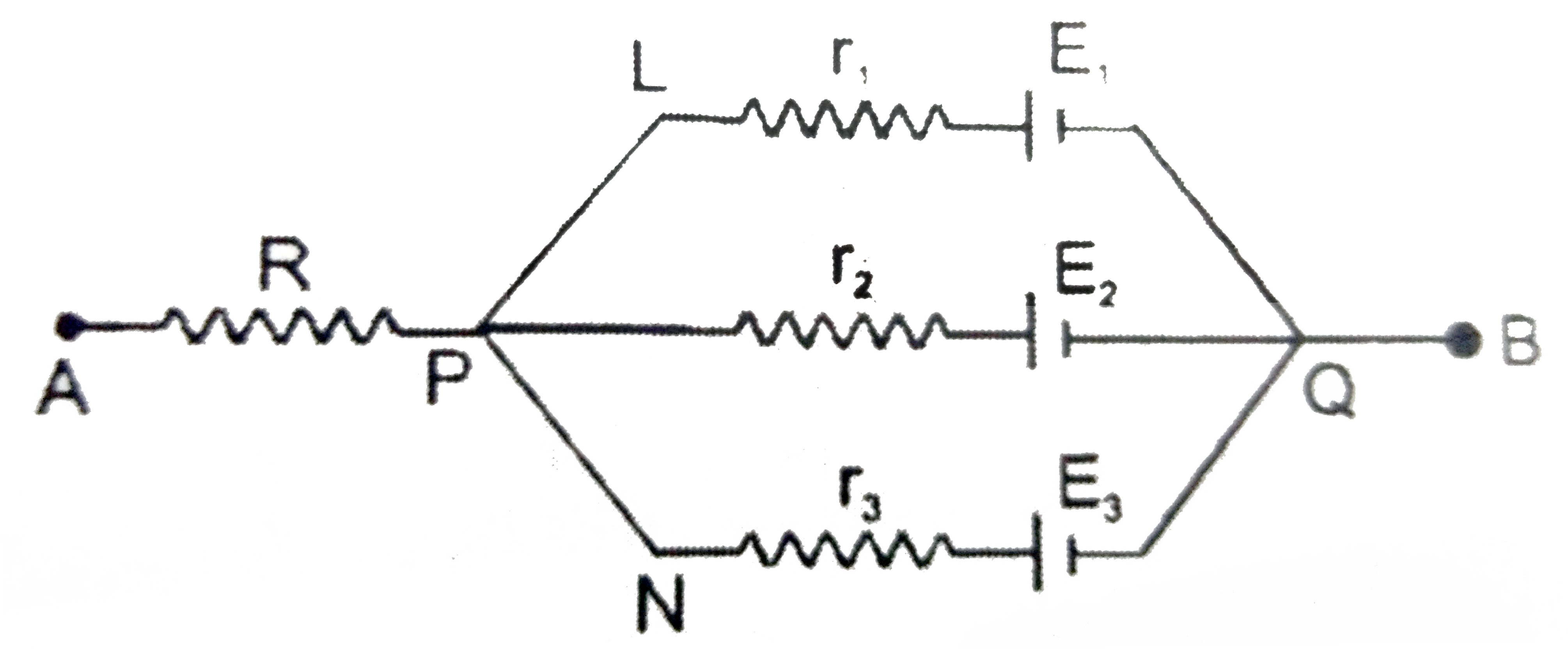
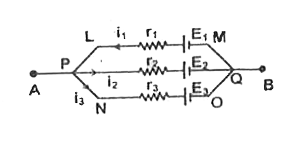
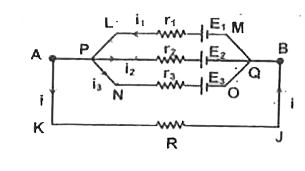
Text Solution

Verified by Experts

Applying Kirchoff.s loop law to mesh PLMQP and PLMQONP in the figure shown below, we  have
`i_(1)r_(1)+i_(2)r_(2)=E_(1)-E_(2)ori,+i_(2)=1ldots(i)`
`i_(1)r_(1)+i_(3)r_(3)=E_(1)-E_(3)ori-(1)+i-(3)=2ldots`(ii)`AtP,i_(2)+i_(3)=i_(1)`ldots(iii)
On solving (i), (ii) and (iii) `i_(1) = 1 amp. i_(2) = 0 amp. i_(3) = 1 amp`

Since no current is drawn along the branch APtherefore`V_(AB) = V_(PQ)`
Potential difference across PQ, ,br>`V_(PQ) = E_(1) -i_(1)r_(1)=2Votl`
(b) The figure shows the circuit when point A is connected to point B and `r_(2)` is short-circuited.Applying Kirchoff.s junction rule at P, we get`i = i_(1) + i_(2) +i_(3)`ldots(iv)
Applying Kirchoff.s law to mesh ABMLA `i-(1)r_(1) = E_(1)-E_(2) or i_(1) = 1 amp`
Applying Kirchoff.s law to mesh ANOQML`i_1r_(1)-i_(3)r_(3)=E_(1)-E_(3)ori_(1)+I_(2)+I_(3)=2ldots(v)`
From above equations `I_(1) = 1 amp, i_(2) = 2 amp, i_(3) = -1 amp`
.lamp (direction of current is opposite)
So, current through resistor R will be `l = I_(1)+l_(2)+ I_(3) = 2 amp`
Promotional Banner

Topper's Solved these Questions

  • CURRENT ELECTRICITY

    FIITJEE|Exercise SOLVED PROBLEMS (SUBJECTIVE)|10 Videos

  • CURRENT ELECTRICITY

    FIITJEE|Exercise SOLVED PROBLEMS (OBJECTIVE)|20 Videos

  • CURRENT ELECTRICITY

    FIITJEE|Exercise Comprehension -4|3 Videos

  • COLLISION

    FIITJEE|Exercise (NUMERICAL BASED QUESTIONS)|4 Videos

  • ELASTICITY AND WAVES

    FIITJEE|Exercise Assignment Problems (Objective) Level-II|15 Videos

Similar Questions

Explore conceptually related problems

In the circuit shown in fig E_1 = 3 volts, E_2 = 2volts, E_3 = 1volt and R = r_1 = r_2= r_3= 1 ohm. (i) Find the potential difference between the points A and B and the currents through each branch. (ii) If r_2 is short circuited and the point A is connected to point B, find the current through E_1, E_2, E_3 and the resistor R.

In the circuit as shown in figure, E_(1)=2V , E_(2)=2V, E_(3)=1V, and R=r_(1)=r_(2)=r_(3)Omega . The potential difference between points A and B will be

In the circuit in figure E_1=3V, E_2=2V, E_3=1V and R=r_1-r_2-r_3=1Omega a. Find the potential differece between the points A and B and the currents through each branch. b. If r_2 is short circuited and the point A is connected to point B , find the currents through E_1,E_2, E_3 and the resistor R

In the circuit shown in figure , (epsilon)_(1)=3V,(epsilon)_(2)=2V,(epsilon)_(3)=1V and r_(1)=r_(2)=r_(3)=1(Omega) .Find the potential difference between the points A and B and the current through each branch.

In the circuit shown in figure E_1=10 V, E_2=4V, r_1=r_2=1Omega and R=2Omega . Find the potential difference across battery 1 and battery 2.

If the circuit a potential difference of 3V is required between the point C and D . Find the value of resistance r_(2)

In the circuit shown here, E_(1) = E_(2) = E_(3) = 2 V and R_(1) = R_(2) = 4 ohms . The current flowing between point A and B through battery E_(2) is

In the circuit shown in fig. 5.265, E_1 = E_2 = E_3 = 2V and R_1 = R_2 = 4Omega. The current flowing between points A and B through battery E_2 is