Home
Class 12
MATHS
The center of a square is at the origin ...

The center of a square is at the origin and its one vertex is `A(2,1)dot` Find the coordinates of the other vertices of the square.

Text Solution

Verified by Experts

The correct Answer is:
(-2,1), (-1,2) and (1,-2)

ABCD is square having centre at origin.
Clearly, `C-=(-2,-1)`
`AO = sqrt(5)`
`"Slope of AO" = (1-0)/(2-0) = (1)/(2)`
`therefore " Slope of BD" =-2`
`rArr -2="tan" theta`
`therefore " cos" theta=-(1)/(sqrt(5)) " and sin" theta = (2)/(sqrt(5))`
Since B and D are on BD at a distance `sqrt(5)` from O, their coordinates (in some order) will be
`(0+-sqrt(5) "cos" theta, 0+-sqrt(5) "sin" theta)`
`(0overset(-)(+)1,0 +-2)`
or (-1,2 and (1,-2)
Promotional Banner

Topper's Solved these Questions

  • STRAIGHT LINES

    CENGAGE|Exercise Exercise 2.3|7 Videos

  • STRAIGHT LINES

    CENGAGE|Exercise Exercise 2.4|8 Videos

  • STRAIGHT LINES

    CENGAGE|Exercise Exercise 2.1|23 Videos

  • STRAIGHT LINE

    CENGAGE|Exercise Multiple Correct Answers Type|8 Videos

  • THEORY OF EQUATIONS

    CENGAGE|Exercise JEE Advanced Previous Year|9 Videos

Similar Questions

Explore conceptually related problems

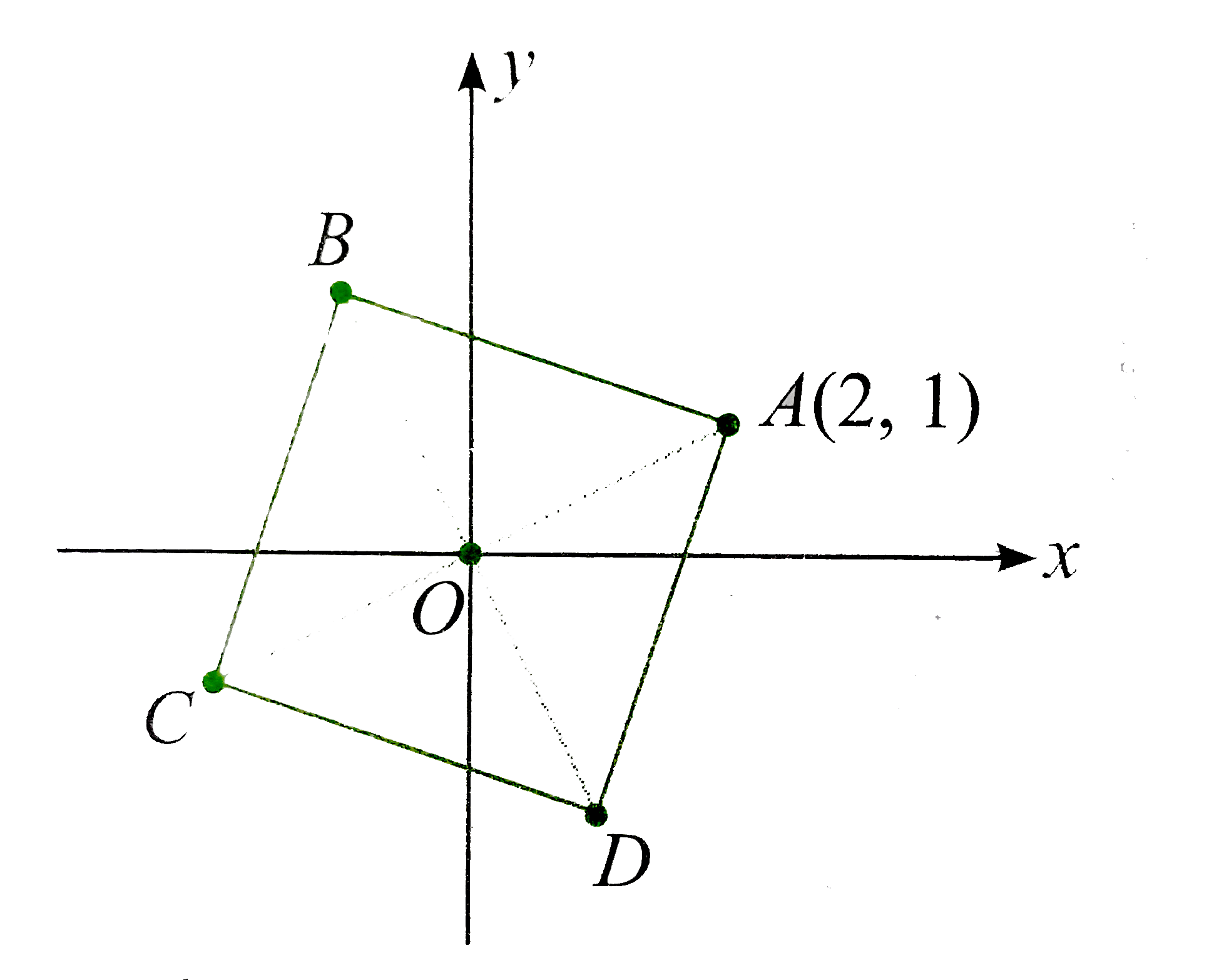
The center of a square is at the origin and its one vertex is A(2,1). Find the coordinates of the other vertices of the square.

Each side of a square is of length 6 units and the centre of the square Is (-1,2). One of its diagonals is parallel to x+y=0. Find the co- ordinates of the vertices of the square.

Two opposite vertices of a square are (0, -2) (2,6) . Find the coordinates of the other vertices.

The centre of a square is at the origin and one of the vertex is 1-i extremities of diagonal not passing through this vertex are

A vertex of a square is at the origin and its one side lies along the line 3x-4y-10=0. Find the area of the square.

A cube of side 5 has one vertex at the point (1,0,1) and the three edges from this vertex are respectively,parallel to the negative x and y axes and positive z-axis.Find the coordinates of the other vertices of the cube.

The opposite vertices of a square are (2, 6) and (0, -2). Find the coordinates of the other vertices.

The two opposite vertices of a square are (3, 4) and (1, -1). Find the co-ordinates of the other two vertices.

Q.7 The two opposite vertices of a square are (1.-6) and (5,4). Find the coordinates of the other two vertices.